题目内容
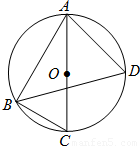
(几何证明选讲选选做题)如图,圆的两条弦AC、BD相交于P,弧AB、BC、CD、DA的度数分别为60°、105°、90°、105°,则 = .
= .
【答案】分析:根据弧AB、CD、的度数分别为60°、90°,得到弦AB的长度等于半径,弦CD的长度等于半径的 倍,根据两个三角形的两对角对应相等,得到两个三角形相似,得到对应边成比例,得到结果.
倍,根据两个三角形的两对角对应相等,得到两个三角形相似,得到对应边成比例,得到结果.
解答:解:连接AB,CD
∵弧AB、CD、的度数分别为60°、90°,
∴弦AB的长度等于半径,弦CD的长度等于半径的 倍,
倍,
即 ,
,
∵∠A=∠D,∠C=∠B,
∴△ABP∽△CDP
∴
∴ ,
,
故答案为:
点评:本题解题时注意不要把圆上的弦长之比直接等于弧长之比,本题所给的两段弧的度数是两个特殊的弧度,要根据弧度之比得到弦长之比,不要出错.
 倍,根据两个三角形的两对角对应相等,得到两个三角形相似,得到对应边成比例,得到结果.
倍,根据两个三角形的两对角对应相等,得到两个三角形相似,得到对应边成比例,得到结果.解答:解:连接AB,CD
∵弧AB、CD、的度数分别为60°、90°,
∴弦AB的长度等于半径,弦CD的长度等于半径的
 倍,
倍,即
 ,
,∵∠A=∠D,∠C=∠B,
∴△ABP∽△CDP
∴

∴
 ,
,故答案为:

点评:本题解题时注意不要把圆上的弦长之比直接等于弧长之比,本题所给的两段弧的度数是两个特殊的弧度,要根据弧度之比得到弦长之比,不要出错.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
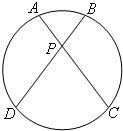 (几何证明选讲选选做题)如图,圆的两条弦AC、BD相交于P,弧AB、BC、CD、DA的度数分别为60°、105°、90°、105°,则
(几何证明选讲选选做题)如图,圆的两条弦AC、BD相交于P,弧AB、BC、CD、DA的度数分别为60°、105°、90°、105°,则 (几何证明选讲选选做题)如图,AC是⊙O的直径,B是⊙O上一点,∠ABC的平分线与⊙O相交于.D已知BC=1,AB=
(几何证明选讲选选做题)如图,AC是⊙O的直径,B是⊙O上一点,∠ABC的平分线与⊙O相交于.D已知BC=1,AB=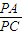 = .
= .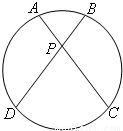
 ,则AD= ;过B、D分别作⊙O的切线,则这两条切线的夹角θ= .
,则AD= ;过B、D分别作⊙O的切线,则这两条切线的夹角θ= .