题目内容
选修4-2:矩阵与交换
已知二阶矩阵M=
,矩阵M对应的变换将点(2,1)变换成点(4,-1).求矩阵M将圆x2+y2=1变换后的曲线方程.
已知二阶矩阵M=
|
分析:根据矩阵M对应的变换将点(2,1)变换成点(4,-1),可求得M=
.在单位圆上设点P(x,y),P被M变换后变成曲线C上的点Q(x',y'),利用矩阵变换的公式列方程组,并将x、y表示成x'、y'的式子,将此关系式作为点P坐标,代入单位圆方程,化简整理即得变换后的曲线C方程.
|
解答:解:∵二阶矩阵M=
,矩阵M对应的变换将点(2,1)变换成点(4,-1).
∴M
=
,即
•
=
可得
,解之得
,所以M=
设点P(x,y)是圆x2+y2=1上的任意一点,变换后的点为Q(x',y'),则
M
=
,可得
,从而
将点P(
(x'-2y'),
(x'+y'))代入单位圆方程,得
(x'-2y')2+
(x'+y')2=1,化简整理得:2(x')2+5(y')2-2x'y'-9=0
∴M将圆x2+y2=1变换后的曲线C方程为:2x2+5y2-2xy-9=0.
|
∴M
|
|
|
|
|
可得
|
|
|
设点P(x,y)是圆x2+y2=1上的任意一点,变换后的点为Q(x',y'),则
M
|
|
|
|
将点P(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 9 |
∴M将圆x2+y2=1变换后的曲线C方程为:2x2+5y2-2xy-9=0.
点评:本题给出矩阵M,叫我们求单位圆经M变换后的曲线的方程,着重考查了矩阵的乘法法则和矩阵变换的含义等知识,属于基础题.

练习册系列答案
相关题目
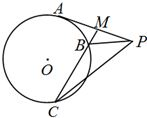 选做题本题包括A,B,C,D四小题,请选定其中 两题 作答,每小题10分,共计20分,
选做题本题包括A,B,C,D四小题,请选定其中 两题 作答,每小题10分,共计20分,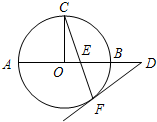 A(选修4-1:几何证明选讲)
A(选修4-1:几何证明选讲) 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.解答应写出文字说明、证明过程或演算步骤. [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.