题目内容
若数列{an}(an∈R)对任意的正整数m,n满足am+n=aman,且a3=2
,那么a10=( )
| 2 |
分析:由数列{an}(an∈R)对任意的正整数m,n满足am+n=aman,取n=m=1,可得a2=a1a1.再取m=2,n=1,可得a3=a2a1=
,解得a1.取m=1,可得an+1=ana1,可得:数列{an}是等比数列,利用等比数列的通项公式即可得出.
| a | 3 1 |
解答:解:由数列{an}(an∈R)对任意的正整数m,n满足am+n=aman,取n=m=1,可得a2=a1a1,
再取m=2,n=1,可得a3=a2a1=
=2
,解得a1=
.
取m=1,可得an+1=ana1=
an,
∴数列{an}是等比数列,首项为
,公比为
.
∴an=
×(
)n-1=(
)n.
∴a10=(
)10=25=32.
故选C.
再取m=2,n=1,可得a3=a2a1=
| a | 3 1 |
| 2 |
| 2 |
取m=1,可得an+1=ana1=
| 2 |
∴数列{an}是等比数列,首项为
| 2 |
| 2 |
∴an=
| 2 |
| 2 |
| 2 |
∴a10=(
| 2 |
故选C.
点评:本题考查了递推数列的意义、等比数列的通项公式,属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目

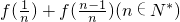 的值;
的值;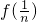 +
+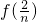 +…+
+…+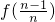 +f(1)(n∈N*),求数列{an}的通项公式;
+f(1)(n∈N*),求数列{an}的通项公式;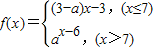 ,若数列{an}满足an=f(n)(n∈N+)且对任意的两个正整数m,n(m≠n)都有(m-n)(am-an)>0,那么实数a的取值范围是( )
,若数列{an}满足an=f(n)(n∈N+)且对任意的两个正整数m,n(m≠n)都有(m-n)(am-an)>0,那么实数a的取值范围是( ) ,3)
,3) ,3)
,3)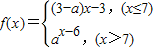 ,若数列{an}满足an=f(n)(n∈N+)且对任意的两个正整数m,n(m≠n)都有(m-n)(am-an)>0,那么实数a的取值范围是( )
,若数列{an}满足an=f(n)(n∈N+)且对任意的两个正整数m,n(m≠n)都有(m-n)(am-an)>0,那么实数a的取值范围是( ) ,3)
,3) ,3)
,3)