题目内容
7.已知命题p:?x∈R,使得x2-2x+m<0,命题q:方程$\frac{{x}^{2}}{m+1}$+$\frac{{y}^{2}}{2-m}$=1表示椭圆.(Ⅰ)写出命题p的否定形式;
(Ⅱ)若命题p∨q为真,求实数m的取值范围.
分析 (I)利用¬p定义即可得出;
(II)命题p:?x∈R,使得x2-2x+m<0,可得△=4-4m≥0,解得m.命题q:方程$\frac{{x}^{2}}{m+1}$+$\frac{{y}^{2}}{2-m}$=1表示椭圆,可得$\left\{\begin{array}{l}{m+1>0}\\{2-m>0}\\{m+1≠2-m}\end{array}\right.$,解得m范围.由命题p∨q为真,
求其并集即可得出.
解答 解:(I)¬p:?x∈R,使得x2-2x+m≥0.
(II)∵命题p:?x∈R,使得x2-2x+m<0,∴△=4-4m≥0,解得m≤1.
命题q:方程$\frac{{x}^{2}}{m+1}$+$\frac{{y}^{2}}{2-m}$=1表示椭圆,∴$\left\{\begin{array}{l}{m+1>0}\\{2-m>0}\\{m+1≠2-m}\end{array}\right.$,解得-1<m<2,且m$≠\frac{1}{2}$.
∵命题p∨q为真,
∴m<2.
故实数m的取值范围是m<2.
点评 本题考查了简易逻辑的判定方法、一元二次不等式的解法、椭圆的标准方程,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.已知b是实数,若$\frac{1+bi}{2-i}$是纯虚数,则b=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
15.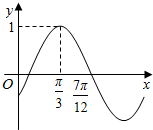 已知函数f(x)=sin(ωx+φ)($ω>0,|φ|<\frac{π}{2}$)的部分图象如图所示,则y=f(x)的图象可由y=cosωx的图象( )
已知函数f(x)=sin(ωx+φ)($ω>0,|φ|<\frac{π}{2}$)的部分图象如图所示,则y=f(x)的图象可由y=cosωx的图象( )
 已知函数f(x)=sin(ωx+φ)($ω>0,|φ|<\frac{π}{2}$)的部分图象如图所示,则y=f(x)的图象可由y=cosωx的图象( )
已知函数f(x)=sin(ωx+φ)($ω>0,|φ|<\frac{π}{2}$)的部分图象如图所示,则y=f(x)的图象可由y=cosωx的图象( )| A. | 向右平移$\frac{π}{3}$个长度单位 | B. | 向左平移$\frac{π}{3}$个长度单位 | ||
| C. | 向右平移$\frac{π}{6}$个长度单位 | D. | 向左平移$\frac{π}{6}$个长度单位 |
12.下列命题错误的是( )
| A. | 命题“若x2+y2=0,则x=y=0”的逆否命题为“若x,y中至少有一个不为0则x2+y2≠0” | |
| B. | 若命题p:?x0∈R,x02-x0+1≤0,则¬p:?x∈R,x2-x+1>0 | |
| C. | △ABC中,sinA>sinB是A>B的充要条件 | |
| D. | 若向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$>0,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为锐角 |
19.已知集合M={x|x2+px+2=0},N={x|x2-x-q=0}且M∩N={2},则p,q的值为( )
| A. | p=-3,q=-2 | B. | p=-3,q=2 | C. | p=3,q=-2 | D. | p=3,q=2 |
16.在等差数列{an}中,a1>0,5a5=9a9,则当数列{an}的前n项和Sn取最大值时n的值等于( )
| A. | 12 | B. | 13 | C. | 14 | D. | 13或14 |
17.若圆x2+y2-4x-4y-10=0上至少有三个不同的点,到直线l:y=x+b的距离为2$\sqrt{2}$,则b取值范围为( )
| A. | (-2,2) | B. | [-2,2] | C. | [0,2] | D. | [-2,2) |