题目内容
已知二次函数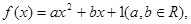 函数
函数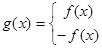
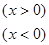
(1)若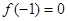 且函数
且函数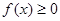 恒成立,求
恒成立,求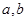 的值;
的值;
(2)在(1)的条件下,当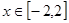 时,
时,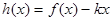 是单调函数,求
是单调函数,求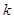 的取值范围.
的取值范围.
(3)若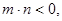
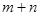 >0,
>0,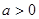 且
且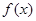 为偶函数,判断
为偶函数,判断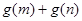 的符号(正或负)
的符号(正或负)
并说明理由.
【答案】
(1) (2)
(2) (3)
(3)
【解析】(1) 由已知 且函数
且函数 恒成立,可转化为
恒成立,可转化为 .解方程组即可.
.解方程组即可.
(2)由题意可知 ,然后可利用二次函数的性质建立关于k的不等式求解.要注意此区间可能为增区间,也可能为减区间.
,然后可利用二次函数的性质建立关于k的不等式求解.要注意此区间可能为增区间,也可能为减区间.
(3)首先根据f(x)为偶函数,可确定b=0,然后由
 ,
, ,可得
,可得 故
故 ,从而可得
,从而可得 ,
, 
然后再研究g(m)+g(n)的符合即可.
解:(1)由已知 且函数
且函数 恒成立,
恒成立,
所以 解得:
解得: ………3分
………3分
(2)由(1) 又
又
所以
因为当 时,
时, 是单调函数
是单调函数
所以 或
或 即
即
所以 的取值范围是
的取值范围是 ………7分
………7分
(3)因为 为偶函数,
为偶函数,
即

 所以
所以

又
 >0,
>0,
所以 故
故

所以



=
所以 ………12分
………12分

练习册系列答案
相关题目
 已知二次函数f(x)=ax2+bx+c,直线l1:y=-t2+8t(其中0≤t≤2,t为常数);l2:x=2.若直线l1、l2与函数f(x)的图象以及l1、y轴所围成的封闭图形如阴影所示.
已知二次函数f(x)=ax2+bx+c,直线l1:y=-t2+8t(其中0≤t≤2,t为常数);l2:x=2.若直线l1、l2与函数f(x)的图象以及l1、y轴所围成的封闭图形如阴影所示. 已知二次函数f(x)=3x2-3x直线l1:x=2和l2:y=3tx,其中t为常数且0<<1.直线l2与函数f(x)的图象以及直线l1、l2与函数f(x)的图象围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为S(t).
已知二次函数f(x)=3x2-3x直线l1:x=2和l2:y=3tx,其中t为常数且0<<1.直线l2与函数f(x)的图象以及直线l1、l2与函数f(x)的图象围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为S(t).