题目内容
设定义域为[x1,x2]的函数y=f(x)的图象为C,图象的两个端点分别为A、B,点O为坐标原点,点M是C上任意一点,向量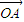 =(x1,y1),
=(x1,y1),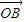 =(x2,y2),
=(x2,y2),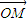 =(x,y),满足x=λx1+(1-λ)x2(0<λ<1),又有向量
=(x,y),满足x=λx1+(1-λ)x2(0<λ<1),又有向量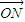 =λ
=λ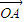 +(1-λ)
+(1-λ)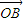 ,现定义“函数y=f(x)在[x1,x2]上可在标准k下线性近似”是指|
,现定义“函数y=f(x)在[x1,x2]上可在标准k下线性近似”是指|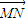 |≤k恒成立,其中k>0,k为常数.根据上面的表述,给出下列结论:
|≤k恒成立,其中k>0,k为常数.根据上面的表述,给出下列结论:①A、B、N三点共线;
②直线MN的方向向量可以为
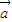 =(0,1);
=(0,1);③“函数y=5x2在[0,1]上可在标准1下线性近似”;
④“函数y=5x2在[0,1]上可在标准
 下线性近似”.
下线性近似”.其中所有正确结论的番号为 .
【答案】分析:由条件推出 ,故①成立;说明M,N的横坐标相同即可;对于函数y=5x2在[0,1]上,求出M(1-λ,5(1-λ)2),N(1-λ,5(1-λ)),|
,故①成立;说明M,N的横坐标相同即可;对于函数y=5x2在[0,1]上,求出M(1-λ,5(1-λ)2),N(1-λ,5(1-λ)),| |=
|= ≤
≤ ,故④成立,③不成立,从而得到答案.
,故④成立,③不成立,从而得到答案.
解答:解:由 =λ
=λ +(1-λ)
+(1-λ) ,得
,得 ,即
,即 故①成立;
故①成立;
∵向量 =(x1,y1),
=(x1,y1), =(x2,y2),向量
=(x2,y2),向量 =λ
=λ +(1-λ)
+(1-λ) ,
,
∴向量 的横坐标为λx1+(1-λ)x2(0<λ<1),
的横坐标为λx1+(1-λ)x2(0<λ<1),
∵ =(x,y),满足x=λx1+(1-λ)x2(0<λ<1),
=(x,y),满足x=λx1+(1-λ)x2(0<λ<1),
∴MN∥y轴
∴直线MN的方向向量可以为 =(0,1),故②成立
=(0,1),故②成立
对于函数y=5x2在[0,1]上,易得A(0,0),B(1,5),
所以M(1-λ,5(1-λ)2),N(1-λ,5(1-λ)),
从而 =
= ≤
≤ ,
,
故函数y=5x2在[0,1]上可在标准 下线性近似”,故④成立,③不成立,
下线性近似”,故④成立,③不成立,
故答案为:①②④
点评:本题考查两个向量坐标形式的运算,求出M(1-λ,5(1-λ)2),N(1-λ,5(1-λ)),正确理解新定义是解题的关键.
 ,故①成立;说明M,N的横坐标相同即可;对于函数y=5x2在[0,1]上,求出M(1-λ,5(1-λ)2),N(1-λ,5(1-λ)),|
,故①成立;说明M,N的横坐标相同即可;对于函数y=5x2在[0,1]上,求出M(1-λ,5(1-λ)2),N(1-λ,5(1-λ)),| |=
|= ≤
≤ ,故④成立,③不成立,从而得到答案.
,故④成立,③不成立,从而得到答案.解答:解:由
 =λ
=λ +(1-λ)
+(1-λ) ,得
,得 ,即
,即 故①成立;
故①成立;∵向量
 =(x1,y1),
=(x1,y1), =(x2,y2),向量
=(x2,y2),向量 =λ
=λ +(1-λ)
+(1-λ) ,
,∴向量
 的横坐标为λx1+(1-λ)x2(0<λ<1),
的横坐标为λx1+(1-λ)x2(0<λ<1),∵
 =(x,y),满足x=λx1+(1-λ)x2(0<λ<1),
=(x,y),满足x=λx1+(1-λ)x2(0<λ<1),∴MN∥y轴
∴直线MN的方向向量可以为
 =(0,1),故②成立
=(0,1),故②成立对于函数y=5x2在[0,1]上,易得A(0,0),B(1,5),
所以M(1-λ,5(1-λ)2),N(1-λ,5(1-λ)),
从而
 =
= ≤
≤ ,
,故函数y=5x2在[0,1]上可在标准
 下线性近似”,故④成立,③不成立,
下线性近似”,故④成立,③不成立,故答案为:①②④
点评:本题考查两个向量坐标形式的运算,求出M(1-λ,5(1-λ)2),N(1-λ,5(1-λ)),正确理解新定义是解题的关键.

练习册系列答案
相关题目
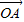 =(x1,y1),
=(x1,y1),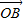 =(x2,y2),
=(x2,y2),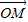 =(x,y),满足x=λx1+(1-λ)x2(0<λ<1),又有向量
=(x,y),满足x=λx1+(1-λ)x2(0<λ<1),又有向量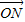 =λ
=λ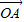 +(1-λ)
+(1-λ)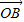 ,现定义“函数y=f(x)在[x1,x2]上可在标准k下线性近似”是指|
,现定义“函数y=f(x)在[x1,x2]上可在标准k下线性近似”是指|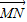 |≤k恒成立,其中k>0,k为常数.根据上面的表述,给出下列结论:①A、B、N三点共线;②“函数y=5x2在[0,1]上可在标准1下线性近似”; ③“函数y=5x2在[0,1]上可在标准
|≤k恒成立,其中k>0,k为常数.根据上面的表述,给出下列结论:①A、B、N三点共线;②“函数y=5x2在[0,1]上可在标准1下线性近似”; ③“函数y=5x2在[0,1]上可在标准 下线性近似”. 其中所有正确结论的序号为( )
下线性近似”. 其中所有正确结论的序号为( )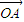 =(x1,y1),
=(x1,y1),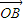 =(x2,y2),
=(x2,y2), =(x,y),满足x=λx1+(1-λ)x2(0<λ<1),又有向量
=(x,y),满足x=λx1+(1-λ)x2(0<λ<1),又有向量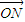 =λ
=λ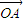 +(1-λ)
+(1-λ)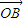 ,现定义“函数y=f(x)在[x1,x2]上可在标准k下线性近似”是指|
,现定义“函数y=f(x)在[x1,x2]上可在标准k下线性近似”是指|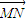 |≤k恒成立,其中k>0,k为常数.根据上面的表述,给出下列结论:
|≤k恒成立,其中k>0,k为常数.根据上面的表述,给出下列结论: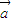 =(0,1);
=(0,1); 下线性近似”.
下线性近似”.