题目内容
.已知函数 (
( 为常数),直线l与函数
为常数),直线l与函数 的图象都相切,且l与函数
的图象都相切,且l与函数 的图象的切点的横坐标为1.
的图象的切点的横坐标为1.

(1)求直线l的方程及a的值;(2)当k>0时,试讨论方程 的解的个数.
的解的个数.
【答案】
(1) 比较①和②的系数得 .
.
|
|
 .
.
(2)(1)当 时有两个解;
(2)当
时有两个解;
(2)当 时有3个解;
时有3个解;
(3)当 时有4个解 (4)当k=ln2时有2个解;
时有4个解 (4)当k=ln2时有2个解;
(5)当 时无解.
时无解.
【解析】(1)先根据 ,可表示出切点(1,0),可求出切线方程,然后再利用此切线方程与y=g(x)也相切可建立关于a的方程,求出a值.
,可表示出切点(1,0),可求出切线方程,然后再利用此切线方程与y=g(x)也相切可建立关于a的方程,求出a值.
(2)解本小题的关键是
然后设 ,再利用导数研究y1的图像特征,作出草图,从图上观察当直线y2=k与y1的不同交点个数时,k的取值范围.
,再利用导数研究y1的图像特征,作出草图,从图上观察当直线y2=k与y1的不同交点个数时,k的取值范围.
(1)
比较①和②的系数得 .
.
(2)

|
|
-1 |
(-1,0) |
0 |
(0,1) |
1 |
|
|
+ |
0 |
- |
0 |
+ |
0 |
- |
|
↗ |
极大值ln2 |
↘ |
极小值 |
↗ |
极大值ln2 |
↘ |
由函数 在R上各区间上的增减及极值情况,可得
在R上各区间上的增减及极值情况,可得
(1)当 时有两个解;
(2)当
时有两个解;
(2)当 时有3个解;
时有3个解;
(3)当 时有4个解 (4)当k=ln2时有2个解;
时有4个解 (4)当k=ln2时有2个解;
(5)当 时无解.
时无解.

练习册系列答案
相关题目


































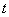




 (
( 为常数,
为常数, 且
且 )的图象过点
)的图象过点 .
. ,试判断函数
,试判断函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.  (
( 为常数,
为常数, ),满足
),满足 ,且
,且 有两个相同的解。
有两个相同的解。 的表达式;
的表达式; 满足
满足 ,且
,且 ,求证:数列
,求证:数列 是等差数列。
是等差数列。 (
( 为常数),直线l与函数
为常数),直线l与函数 的图象都相切,且l与函数
的图象都相切,且l与函数 的图象的切点的横坐标为l.
的图象的切点的横坐标为l. 的解的个数.
的解的个数.