题目内容
设函数f(x)=x(x-1)(x-a)(a∈R),f(x)的两个极值点为A(α,f(α)),B(β,f(β)),线段AB的中点为M.(1)如果函数f(x)为奇函数,求实数a的值;当a=2时,求函数f(x)图象的对称中心;
(2)如果M点在第四象限,求实数a的范围;
(3)证明:点M也在函数f(x)的图象上,且M为函数f(x)图象的对称中心.
【答案】分析:(1)【法一】取特殊值,求得a=-1,再验证f(x)为奇函数;
【法二】利用奇函数的定义,可求a的值;当a=2时,利用图象的变换,可得数f(x)=x(x-1)(x-2)图象的对称中心;
(2)求导数,可得α,β为3x2-2(1+a)x+a=0两实根,再利用韦达定理确定M的坐标,利用M点在第四象限,建立不等式组,即可求实数a的范围;
(3)证明点M也在函数f(x)的图象上.【法一】设P(x,y)为函数f(x)的图象上任意一点,证明P(x,y)关于M的对称点在函数f(x)=x(x-1)(x-a)的图象上;
【法二】利用图象的变换证明结论即可.
解答:(1)解:【法一】因为f(x)为奇函数,所以f(-1)=-f(1),得:-1•(-1-1)(-1-a)=0,∴a=-1.
当a=-1时,f(x)=x(x-1)(x+1)=x(x2-1),有f(-x)=-f(x),则f(x)为奇函数.…(4分)
【法二】f(x)=x3-(1+a)x2+ax,f(-x)=-f(x)恒成立,(-x)3-(1+a)x2-ax=-x3+(1+a)x2-ax,求得a=-1.
当a=2时,f(x)=x(x-1)(x-2),该图象可由奇函数f(x)=(x+1)x(x-1)的图象向右平移一个单位得到,可知函数f(x)=x(x-1)(x-2)图象的对称中心为(1,0).…(4分)
(2)解:∵f′(x)=3x2-2(1+a)x+a,
令f′(x)=3x2-2(1+a)x+a=0,则α,β为3x2-2(1+a)x+a=0两实根.
∴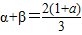 ,
,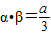 .
.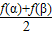 =
=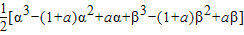
=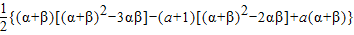
=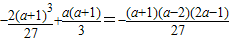 ,
,
∵点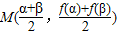 在第四象限,∴
在第四象限,∴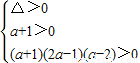
∴a>2或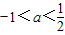 .…(10分)
.…(10分)
(3)证明:由(2)得点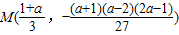 ,
,
又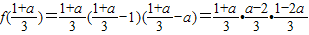 =
=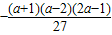 ,
,
所以点M也在函数f(x)的图象上.…(12分)
【法一】设P(x,y)为函数f(x)的图象上任意一点,P(x,y)关于M的对称点为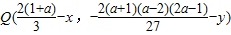
而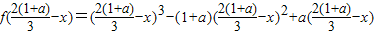
=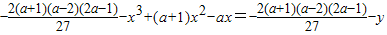 .
.
即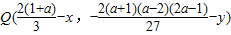 在函数f(x)=x(x-1)(x-a)的图象上.
在函数f(x)=x(x-1)(x-a)的图象上.
所以,M为函数f(x)的对称中心.…(16分)
【法二】设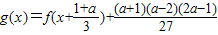 =
=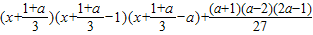 =
=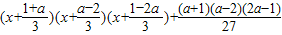 =
=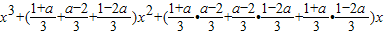
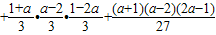 =
=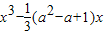 .
.
∴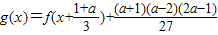 为奇函数,
为奇函数,
对称中心为O(0,0).
把函数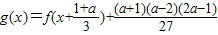 的图象按向量
的图象按向量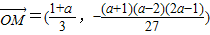 平移后得f(x)的图象,
平移后得f(x)的图象,
∴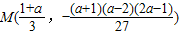 为函数f(x)的对称中心.…(16分)
为函数f(x)的对称中心.…(16分)
点评:本题考查函数的奇偶性与对称性,考查导数知识的运用,考查学生的计算能力,有一定的难度.
【法二】利用奇函数的定义,可求a的值;当a=2时,利用图象的变换,可得数f(x)=x(x-1)(x-2)图象的对称中心;
(2)求导数,可得α,β为3x2-2(1+a)x+a=0两实根,再利用韦达定理确定M的坐标,利用M点在第四象限,建立不等式组,即可求实数a的范围;
(3)证明点M也在函数f(x)的图象上.【法一】设P(x,y)为函数f(x)的图象上任意一点,证明P(x,y)关于M的对称点在函数f(x)=x(x-1)(x-a)的图象上;
【法二】利用图象的变换证明结论即可.
解答:(1)解:【法一】因为f(x)为奇函数,所以f(-1)=-f(1),得:-1•(-1-1)(-1-a)=0,∴a=-1.
当a=-1时,f(x)=x(x-1)(x+1)=x(x2-1),有f(-x)=-f(x),则f(x)为奇函数.…(4分)
【法二】f(x)=x3-(1+a)x2+ax,f(-x)=-f(x)恒成立,(-x)3-(1+a)x2-ax=-x3+(1+a)x2-ax,求得a=-1.
当a=2时,f(x)=x(x-1)(x-2),该图象可由奇函数f(x)=(x+1)x(x-1)的图象向右平移一个单位得到,可知函数f(x)=x(x-1)(x-2)图象的对称中心为(1,0).…(4分)
(2)解:∵f′(x)=3x2-2(1+a)x+a,
令f′(x)=3x2-2(1+a)x+a=0,则α,β为3x2-2(1+a)x+a=0两实根.
∴
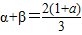 ,
,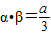 .
.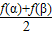 =
=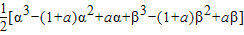
=
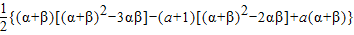
=
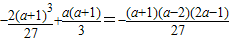 ,
,∵点
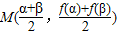 在第四象限,∴
在第四象限,∴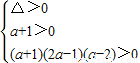
∴a>2或
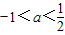 .…(10分)
.…(10分)(3)证明:由(2)得点
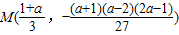 ,
,又
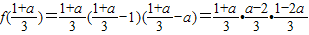 =
=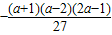 ,
,所以点M也在函数f(x)的图象上.…(12分)
【法一】设P(x,y)为函数f(x)的图象上任意一点,P(x,y)关于M的对称点为
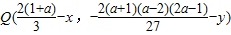
而
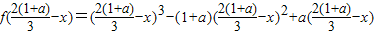
=
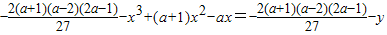 .
.即
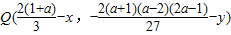 在函数f(x)=x(x-1)(x-a)的图象上.
在函数f(x)=x(x-1)(x-a)的图象上.所以,M为函数f(x)的对称中心.…(16分)
【法二】设
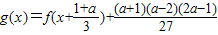 =
=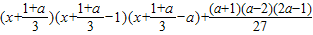 =
=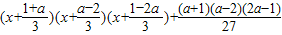 =
=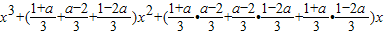
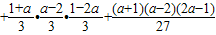 =
=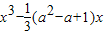 .
.∴
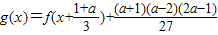 为奇函数,
为奇函数,对称中心为O(0,0).
把函数
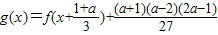 的图象按向量
的图象按向量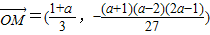 平移后得f(x)的图象,
平移后得f(x)的图象,∴
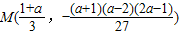 为函数f(x)的对称中心.…(16分)
为函数f(x)的对称中心.…(16分)点评:本题考查函数的奇偶性与对称性,考查导数知识的运用,考查学生的计算能力,有一定的难度.

练习册系列答案
相关题目
设函数f(x)的定义域为A,若存在非零实数t,使得对于任意x∈C(C⊆A),有x+t∈A,且f(x+t)≤f(x),则称f(x)为C上的t低调函数.如果定义域为[0,+∞)的函数f(x)=-|x-m2|+m2,且 f(x)为[0,+∞)上的10低调函数,那么实数m的取值范围是( )
| A、[-5,5] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|