题目内容
已知点P在曲线C1: 上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则|PQ|-|PR|的最大值是( )
上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则|PQ|-|PR|的最大值是( )A.6
B.8
C.10
D.12
【答案】分析:由已知条件可得双曲线的两个焦点为两个圆的圆心,再把|PQ|-|PR|的最大值转化为求|PQ|max-|PR|min即可.
解答:解:由双曲线的知识可知:C1 的两个焦点
的两个焦点
分别是F1(-5,0)与F2(5,0),且|PF1|+|PF2|=8
而这两点正好是两圆(x+5)2+y2=1和(x-5)2+y2=1的圆心,
两圆(x+5)2+y2=4和(x-5)2+y2=1的半径分别是r1=1,r2=1,
∴|PQ|max=|PF1|+1,|PR|min=|PF2|-1,
∴|PQ|-|PR|的最大值为:(|PF1|+1)-(|PF2|-1)
=|PF1|+|PF2|+2=8+2=10,
故选C
点评:本题考查直线与圆锥曲线的综合应用能力,合理地进行等价转化是解决问题的关键.
解答:解:由双曲线的知识可知:C1
 的两个焦点
的两个焦点分别是F1(-5,0)与F2(5,0),且|PF1|+|PF2|=8
而这两点正好是两圆(x+5)2+y2=1和(x-5)2+y2=1的圆心,
两圆(x+5)2+y2=4和(x-5)2+y2=1的半径分别是r1=1,r2=1,
∴|PQ|max=|PF1|+1,|PR|min=|PF2|-1,
∴|PQ|-|PR|的最大值为:(|PF1|+1)-(|PF2|-1)
=|PF1|+|PF2|+2=8+2=10,
故选C
点评:本题考查直线与圆锥曲线的综合应用能力,合理地进行等价转化是解决问题的关键.

练习册系列答案
相关题目
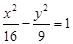 上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则 | PQ |-| PR | 的最大值是
上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则 | PQ |-| PR | 的最大值是 上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则 | PQ |-| PR | 的最大值是
上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则 | PQ |-| PR | 的最大值是