题目内容
已知三次函数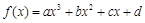 的图象如图所示,则
的图象如图所示,则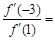 ( )
( )
| A.-1 | B.2 | C.-5 | D.-3 |
C
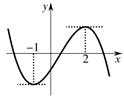
解析试题分析:求导得:f’(x)=3ax2+2bx+c,结合图象可得
x=-1,2为导函数的零点,即f’(-1)=f’(2)=0,
故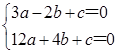 ,解得
,解得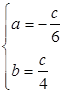 故
故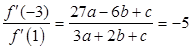 ,故答案为:-5.
,故答案为:-5.
考点:导数的运算;函数的图象..

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数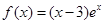 的单调递增区间是 ( )
的单调递增区间是 ( )
A.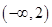 | B.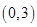 | C.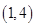 | D.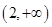 |
已知点P(1,2)是曲线y=2x2上一点,则P处的瞬时变化率为 ( )
| A.2 | B.4 | C.6 | D.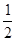 |
已知函数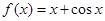 ,则
,则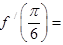 ( )
( )
A.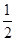 | B.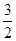 | C.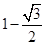 | D.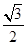 |
曲线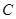 :
: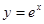 在点
在点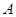 处的切线
处的切线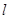 恰好经过坐标原点,则曲线
恰好经过坐标原点,则曲线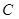 直线
直线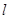 ,
,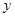 轴围成的图形面积为( )
轴围成的图形面积为( )
A. | B.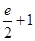 | C.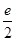 | D.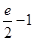 |
若曲线y=x2+ax+b在点(0,b)处的切线方程是x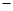 y+1=0,则( )
y+1=0,则( )
A.a=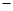 1,b=1 1,b=1 | B.a=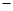 1,b= 1,b=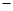 1 1 | C.a=1,b= 1 1 | D.a=1,b=1 |
函数f(x)=x3+ax2+3x﹣9,已知f(x)在x=﹣3时取得极值,则a=( )
| A.2 | B.3 | C.4 | D.5 |
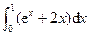 =( )
=( )
| A.1 |
B.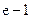 |
| C.e |
| D.1+e |
已知点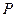 在曲线
在曲线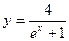 上,
上,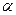 为曲线在点
为曲线在点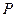 处的切线的倾斜角,则
处的切线的倾斜角,则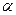 的取值范围是( )
的取值范围是( )
A.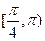 |
B.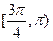 |
C.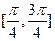 |
D.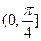 |