题目内容
11．已知某几何体的三视图如图所示（其中正视图为等腰直角三角形），则该几何体的外接球的表面积为（ ）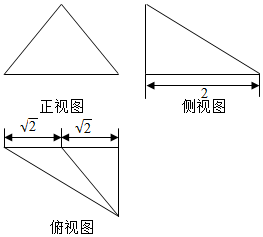
| A． | 12π | B． | 8π | C． | 4π | D． | 2π |
分析 根据几何体的三视图，得出该几何体是侧面垂直于底面，且底面是直角三角形的三棱锥，求出该三棱锥外接球的直径，即可求出外接球的表面积．
解答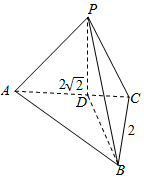 
解：根据几何体的三视图，得；
该几何体是如图所示的三棱锥，
且侧面PAC⊥底面ABC，AC⊥BC，
PA=PC=$\sqrt{{（\sqrt{2}）}^{2}{+（\sqrt{2}）}^{2}}$=2，AC=2$\sqrt{2}$，BC=2；
PB2=PC2+BC2=22+22=8，
AB=$\sqrt{{2}^{2}{+（2\sqrt{2}）}^{2}}$=2$\sqrt{3}$，
∴PA2+PB2=AB2，
∴PA⊥PB，
∴AB是该三棱锥外接球的直径，
∴该外接球的表面积为S=4πR2=π•${（2\sqrt{3}）}^{2}$=12π．
故选：A．
点评 本题考查了空间几何体三视图的应用问题，解题的关键是根据三视图还原出几何体的结构特征，是基础题．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
1．已知抛物线M：y2=12x的焦点F到双曲线C：$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1（a＞0，b＞0）渐近线的距离为$\frac{3\sqrt{10}}{4}$，点P是抛物线M上的一动点，且P到双曲线C的焦点F1（0，c）的距离与到直线x=-3的距离之和的最小值为5，则双曲线C的方程为（ ）
| A． | $\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{4}$=1 | B． | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{12}$=1 | C． | $\frac{{y}^{2}}{6}$-$\frac{{x}^{2}}{10}$=1 | D． | $\frac{{y}^{2}}{10}$-$\frac{{x}^{2}}{6}$=1 |
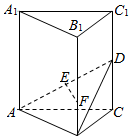在正三棱柱ABC-A1B1C1中，AB=AA1=1，DC=DC1，AE=ED，F为BB1上任意一点，且FB1=3BF．
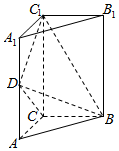如图，底面是直角三角形的直三棱柱ABC-A1B1C1中，$AC=BC=\frac{1}{2}A{A_1}=1$，D是棱AA1上的动点．
如图，直三棱柱ABC-A1B1C1中，∠ACB=90°，AC=BC=$\frac{2}{5}$AA1，D是棱AA1上的点，且AD=$\frac{1}{4}$DA1．