题目内容
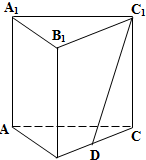 (2009•嘉定区一模)如图,在正三棱柱ABC-A1B1C1中,底面△ABC的边长为2,D为BC的中点,三棱柱的体积V=3
(2009•嘉定区一模)如图,在正三棱柱ABC-A1B1C1中,底面△ABC的边长为2,D为BC的中点,三棱柱的体积V=3| 3 |
(1)求该三棱柱的侧面积;
(2)求异面直线AB与C1D所成角的大小(结果用反三角函数值表示)
分析:(1)由已知中正三棱柱ABC-A1B1C1中,底面△ABC的边长为2,三棱柱的体积V=3
.我们可以计算出棱柱的高,代入到棱柱的侧面积公式,即可求出答案.
(2)取AC中点E,连接DE、C1E,由三角形中位线定理及异面直线夹角的定义,可得∠C1DE(或其补角)就是异面直线AB与C1D所成的角,解△C1DE即可得到异面直线AB与C1D所成角的大小.
| 3 |
(2)取AC中点E,连接DE、C1E,由三角形中位线定理及异面直线夹角的定义,可得∠C1DE(或其补角)就是异面直线AB与C1D所成的角,解△C1DE即可得到异面直线AB与C1D所成角的大小.
解答: 解:(1)因为三棱柱的体积V=3
解:(1)因为三棱柱的体积V=3
,而S底=
×4=
,所以A1A=3…(3分)
所以S侧=3×2×3=18.…(6分)
(2)取AC中点E,连接DE、C1E,
则ED∥AB,所以,∠C1DE(或其补角)就是异面直线AB与C1D所成的角.…(8分)
在△C1DE中,C1D=C1E=
,DE=1,…(9分)
所以cos∠C1DE=
=
.…(12分)
所以,异面直线AB与C1D所成角的大小为arccos
.…(14分)
(或arcsin
,或arctan
)
 解:(1)因为三棱柱的体积V=3
解:(1)因为三棱柱的体积V=3| 3 |
| ||
| 4 |
| 3 |
所以S侧=3×2×3=18.…(6分)
(2)取AC中点E,连接DE、C1E,
则ED∥AB,所以,∠C1DE(或其补角)就是异面直线AB与C1D所成的角.…(8分)
在△C1DE中,C1D=C1E=
| 10 |
所以cos∠C1DE=
| 1 | ||
2
|
| ||
| 20 |
所以,异面直线AB与C1D所成角的大小为arccos
| ||
| 20 |
(或arcsin
| ||
| 20 |
| 39 |
点评:本题考查的知识点是异面直线的夹角,三棱柱的体积和表面积,其中(1)的关键是根据已知求出棱柱的高,(2)的关键是构造出∠C1DE(或其补角)就是异面直线AB与C1D所成的角,将异面直线夹角问题转化为解三角形问题.

练习册系列答案
相关题目
 (2009•嘉定区一模)如图,学校现有一块三角形空地,∠A=60°,AB=2,AC=3(单位:m),现要在此空地上种植花草,为了美观,用一根条形石料DE将空地隔成面积相等的两部分(D在AB上,E在AC上).
(2009•嘉定区一模)如图,学校现有一块三角形空地,∠A=60°,AB=2,AC=3(单位:m),现要在此空地上种植花草,为了美观,用一根条形石料DE将空地隔成面积相等的两部分(D在AB上,E在AC上).