Question

（2009•嘉定区一模）如图，学校现有一块三角形空地，∠A=60°，AB=2，AC=3（单位：m），现要在此空地上种植花草，为了美观，用一根条形石料DE将空地隔成面积相等的两部分（D在AB上，E在AC上）．
（1）设AD=x，AE=y，求用x表示y的函数y=f（x）的解析式，并写出f（x）的定义域；
（2）如何选取D、E的位置，可以使所用石料最省？

Answer 1

分析：（1）由于DE将空地隔成面积相等的两部分，所以可建立方程

1

2

•x•y•sinA=

1

4

•AB•AC•sinA，化简即可得函数y=f（x）的解析式；
（2）选取D、E的位置，可以使所用石料最省，即必须使得DE最短，故利用余弦定理可表示出DE，再利用基本不等式确定最小值．

解答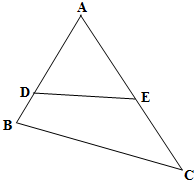：解：（1）由题意得，S_△ADE=S_△ABC，
即

1

2

•x•y•sinA=

1

4

•AB•AC•sinA，…（4分）
解得y=

3

x

，…（5分）
所以f(x)=

3

x

，f（x）的定义域为[1，2]．…（7分）
（2）在△ADE中，由余弦定理得，DE²=AD²+AE²-2•AD•AE•cosADE²=x²+y²-2xycos60°=x²+y²-xy=x2+

9

x2

-3，x∈[1，2]，…（10分）
令x²=t，则t∈[1，4]，于是DE2=t+

9

t

-3≥6-3=3，…（12分）
当且仅当t=3，即x=

3

时，DE²取最小值

3

．…（13分）
所以，当D、E离点A的距离均为

3

m时（或AD=AE=

3

（m）时），DE最短，即所用石料最省．…（14分）

点评：本题的考点是解三角形的实际应用，主要考查三角形的面积公式，考查余弦定理，同时考查了基本不等式的运用，关键是函数关系式的建立，如何将实际问题转化为数学问题．