题目内容
 将数列{an}中的所有项按每一行比上一行多一项的规则排成如下表:
将数列{an}中的所有项按每一行比上一行多一项的规则排成如下表:
记表中的第一列数a1,a2,a4,a7,…,构成的数列为{bn},b1=a1=1,Sn为数列{bn}的前n项和,且满足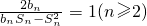 .
.
(1)求证数列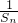 成等差数列,并求数列{bn}的通项公式;
成等差数列,并求数列{bn}的通项公式;
(2)上表中,若a81项所在行的数按从左到右的顺序构成等比数列,且公比q为正数,求当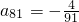 时,公比q的值.
时,公比q的值.
解:(1)由已知,当n≥2时, ,又bn=Sn-Sn-1,(1分)
,又bn=Sn-Sn-1,(1分)
所以 .(2分)
.(2分)
即 ,所以
,所以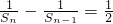 ,(4分)
,(4分)
又S1=b1=a1=1,所以数列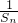 是首项为1,公差为
是首项为1,公差为 的等差数列.(5分)
的等差数列.(5分)
所以 ,即
,即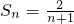 .(7分)
.(7分)
所以,当n≥2时, ,(9分)
,(9分)
因此 (10分)
(10分)
(2)因为 ,
,
所以表中第1行至第12行共含有数列{an}的前78项,故a81在表中第13行第三列.(12分)
所以, ,(13分)
,(13分)
又 ,所以q=2.(14分)
,所以q=2.(14分)
分析:(1)由 ,知
,知 ,所以
,所以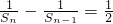 ,由此能够推导出数列{bn}的通项公式.
,由此能够推导出数列{bn}的通项公式.
(2)因为 ,所以表中第1行至第12行共含有数列{an}的前78项,故a81在表中第13行第三列,由此能求出当
,所以表中第1行至第12行共含有数列{an}的前78项,故a81在表中第13行第三列,由此能求出当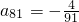 时,公比q的值.
时,公比q的值.
点评:本题考查数列的性质和应用,解题时要灵活运用数列通项公式的求解方法,合理地利用递推公式,仔细审题,认真解答.
 ,又bn=Sn-Sn-1,(1分)
,又bn=Sn-Sn-1,(1分)所以
 .(2分)
.(2分)即
 ,所以
,所以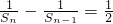 ,(4分)
,(4分)又S1=b1=a1=1,所以数列
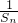 是首项为1,公差为
是首项为1,公差为 的等差数列.(5分)
的等差数列.(5分)所以
 ,即
,即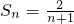 .(7分)
.(7分)所以,当n≥2时,
 ,(9分)
,(9分)因此
 (10分)
(10分)(2)因为
 ,
,所以表中第1行至第12行共含有数列{an}的前78项,故a81在表中第13行第三列.(12分)
所以,
 ,(13分)
,(13分)又
 ,所以q=2.(14分)
,所以q=2.(14分)分析:(1)由
 ,知
,知 ,所以
,所以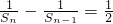 ,由此能够推导出数列{bn}的通项公式.
,由此能够推导出数列{bn}的通项公式.(2)因为
 ,所以表中第1行至第12行共含有数列{an}的前78项,故a81在表中第13行第三列,由此能求出当
,所以表中第1行至第12行共含有数列{an}的前78项,故a81在表中第13行第三列,由此能求出当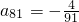 时,公比q的值.
时,公比q的值.点评:本题考查数列的性质和应用,解题时要灵活运用数列通项公式的求解方法,合理地利用递推公式,仔细审题,认真解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
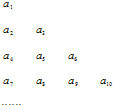 将数列{an}中的所有项按每一行比上一行多一项的规则排成如下表:
将数列{an}中的所有项按每一行比上一行多一项的规则排成如下表:
 将数列{an}中的所有项按每一行比上一行多一项的规则排成如下数表.记表中第一列数a1,a2,a4,a7,…构成的数列为{bn},b1=a1=1.Sn为数列{bn}的前n项和,且满足2bn=bnSn-Sn2(n≥2,n∈N*).
将数列{an}中的所有项按每一行比上一行多一项的规则排成如下数表.记表中第一列数a1,a2,a4,a7,…构成的数列为{bn},b1=a1=1.Sn为数列{bn}的前n项和,且满足2bn=bnSn-Sn2(n≥2,n∈N*).
 (b为大于等于3的正整数),问数列{cn}中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
(b为大于等于3的正整数),问数列{cn}中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.