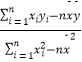Question

【题目】选修4-4：坐标系与参数方程

在平面直角坐标系中，点，直线与动直线的交点为，线段的中垂线与动直线的交点为.

（1）求动点的轨迹的方程；

（2）过动点作曲线的两条切线，切点分别为，，求证：的大小为定值.

Answer 1

【答案】（1）（2）见解析

【解析】试题分析：

(1)由题意可得点的轨迹是抛物线．焦点为，准线为．

所以曲线的方程为．

(2) 由题意，设切线方程为，

联立直线与抛物线方程，由题意可得，所以，为定值．

试题解析：

解:(1) 因为直线与垂直，所以为点到直线的距离．

连结，因为为线段的中垂线与直线的交点，所以．

所以点的轨迹是抛物线．

焦点为，准线为．

所以曲线的方程为．

（2）由题意，过点的切线斜率存在，设切线方程为，

联立 得，

所以，即（*），

因为，所以方程（*）存在两个不等实根，设为，，

因为，所以，为定值．