Question

【题目】已知函数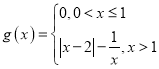，，则方程的实根个数为（ ）

A.2个B.3个C.4个D.5个

Answer 1

【答案】C

【解析】

解,即解.再分与，分别找到函数与在区间、、上的单调性，则可找到方程的实数根的个数.

1），,.

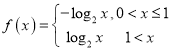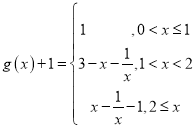①当时，.即在上有1个零点.

②当时，，记，

因为 在 上单调递增，在单调递增，

所以在单调递增,

又，，由零点存在定理知道在上有唯一零点.

③当时，，记,,记，开口向下，且，即恒成立,即，即在上单调递减,

又，即在上存在且有唯一零点.

2），,.

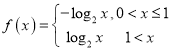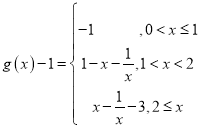①当时，无解.即在上无零点.

②当时，，记，

因为 在 上单调递增，在单调递增，

所以在单调递增,

又，，由零点存在定理知道在上无零点.

③当时，，记,,记，开口向下，且，即恒成立,即，即在上单调递减,

又，即在上存在且有唯一零点.

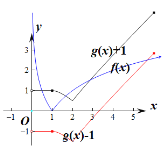
综上所述：方程的实根个数为4个.

故选:C.