题目内容
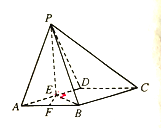
【题目】如图所示,在四棱锥![]() 中,四边形
中,四边形![]() 为菱形,
为菱形, ![]() 为正三角形,且
为正三角形,且![]() 分别为
分别为![]() 的中点,
的中点, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)证明:AD⊥平面PEB,利用四边形ABCD为菱形,可得AD∥BC,即可证明BC⊥平面PEB;
(2)以E为原点,建立坐标系,求出平面PDC的法向量,利用向量的夹角公式,即可求EF与平面PDC所成角的正弦值.
试题解析:
(1)证明:因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() ,
,
又![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
由四边形![]() 菱形,得
菱形,得![]() ,
,
所以![]() 平面
平面![]() .
.
(2)解:
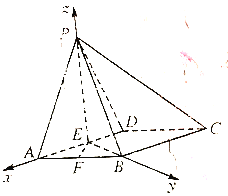
以![]() 为原点,
为原点, ![]() 分别为
分别为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
不妨设菱形![]() 的边长为2,则
的边长为2,则![]() ,
,
![]() ,
,
则点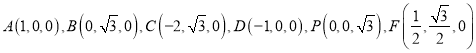 ,
,
![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则由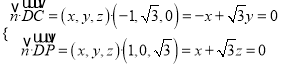 ,解得
,解得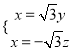 ,
,
不妨令![]() ,得
,得![]() ;
;
又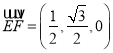 ,
,
所以![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为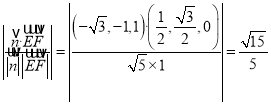 .
.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案【题目】苏州市一木地板厂生产A、B、C三类木地板,每类木地板均有环保型和普通两种型号,某月的产量如下表(单位:片):
类型 | 木地板A | 木地板B | 木地板C |
环保型 | 150 | 200 | Z |
普通型 | 250 | 400 | 600 |
按分层抽样的方法在这个月生产的木地板中抽取50片,其中A类木地板10片.
(1)求Z的值;
(2)用随机抽样的方法从B类环保木地板抽取8片,作为一个样本,经检测它们的得分如下:9.4、8.6、9.2、9.6、8.7、9.3、9.0、8.2,从中任取一个数,求该数与样本平均数之差的绝对不超过0.5的概率.
【题目】宿州某中学N名教师参加“低碳节能你我他”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50),得到的频率分布直方图如图所示. 
下表是年龄的频数分布表:
区间 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50] |
人数 | 25 | m | p | 75 | 25 |
(1)求正整数m,p,N的值;
(2)用分层抽样的方法,从第1、3、5组抽取6人,则第1、3、5组各抽取多少人?
(3)在(2)的条件下,从这6人中随机抽取2人参加学校之间的宣传交流活动,求恰有1人在第3组的概率.