题目内容
已知函数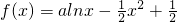 (a>0).
(a>0).
(1)求f(x)的单调区间;
(2)求f(x)在[1,+∞)上的最大值.
解:(1)f(x)的定义域为(0,+∞),f′(x)=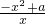 .…(2分)
.…(2分)
令f′(x)=0得x= 或x=-
或x=- (舍).
(舍).
函数f(x),f′(x)随x的变化如下:
所以f(x)的单调递增区间是(0, ),单调递减区间是(
),单调递减区间是( ,+∞).…(6分)
,+∞).…(6分)
(2)由(1)可知:
①当 ≤1,即0<a≤1时,f(x)在[1,+∞)上单调递减.
≤1,即0<a≤1时,f(x)在[1,+∞)上单调递减.
∴fmax(x)=f(1)=0…(9分)
②当 >1,即a>1时,f(x)在[1,
>1,即a>1时,f(x)在[1, )上单调递增,(
)上单调递增,( ,+∞)上单调递减.
,+∞)上单调递减.
∴ …(13分)
…(13分)
分析:(1)求导函数,结合函数的定义域,利用导数的正负,可得f(x)的单调区间;
(2)分类讨论,求得f(x)在[1,+∞)上的单调性,即可求f(x)在[1,+∞)上的最大值.
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的最值,考查分类讨论的数学思想,属于中档题.
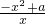 .…(2分)
.…(2分)令f′(x)=0得x=
 或x=-
或x=- (舍).
(舍).函数f(x),f′(x)随x的变化如下:
| x | (0, ) ) |  | ( ,+∞) ,+∞) |
| f′(x) | + | 0 | - |
| f(x) | ↗ | 极大值 | ↘ |
 ),单调递减区间是(
),单调递减区间是( ,+∞).…(6分)
,+∞).…(6分)(2)由(1)可知:
①当
 ≤1,即0<a≤1时,f(x)在[1,+∞)上单调递减.
≤1,即0<a≤1时,f(x)在[1,+∞)上单调递减.∴fmax(x)=f(1)=0…(9分)
②当
 >1,即a>1时,f(x)在[1,
>1,即a>1时,f(x)在[1, )上单调递增,(
)上单调递增,( ,+∞)上单调递减.
,+∞)上单调递减.∴
 …(13分)
…(13分)分析:(1)求导函数,结合函数的定义域,利用导数的正负,可得f(x)的单调区间;
(2)分类讨论,求得f(x)在[1,+∞)上的单调性,即可求f(x)在[1,+∞)上的最大值.
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的最值,考查分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
 ,
, (a>0),若
(a>0),若 ,
, ,使得f(x1)= g(x2),则实数a的取值范围是( )
,使得f(x1)= g(x2),则实数a的取值范围是( ) (B)
(B)
 (C)
(C)
 (D)
(D)

 (a>0,且a≠1)
(a>0,且a≠1) (A>0,ω>0,x∈(-∞,+∞))的最小正周期为π,且
(A>0,ω>0,x∈(-∞,+∞))的最小正周期为π,且 ,则函数y=f(x)在
,则函数y=f(x)在 上的最小值是( )
上的最小值是( )


 其中a>0,e为自然对数的底数。
其中a>0,e为自然对数的底数。
 的单调区间;
的单调区间;