题目内容
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若曲线![]() 和曲线
和曲线![]() 有三个公共点,求以这三个点为顶点的三角形的面积.
有三个公共点,求以这三个点为顶点的三角形的面积.
【答案】(1)![]() ,
,![]() (2)16
(2)16
【解析】分析: (Ⅰ)利用参数方程与普通方程,极坐标方程与直角坐标方程互化的方法,可得曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;(Ⅱ)曲线
的直角坐标方程;(Ⅱ)曲线![]() 和曲线
和曲线![]() 都是关于
都是关于![]() 轴对称的图形,它们有三个公共点,所以原点的它们其中的一个公共点,从而可确定
轴对称的图形,它们有三个公共点,所以原点的它们其中的一个公共点,从而可确定![]() ,进而得到三角形的面积.
,进而得到三角形的面积.
详解: (Ⅰ)曲线![]()
![]() (
(![]() 为参数),消去参数
为参数),消去参数![]() ,得曲线
,得曲线![]() 的普通方程为:
的普通方程为:![]() ,
,
曲线![]() ,即
,即![]() ,化为直角坐标方程为
,化为直角坐标方程为![]() .
.
(Ⅱ)因为曲线![]() 和曲线
和曲线![]() 都是关于
都是关于![]() 轴对称的图形,它们有三个公共点,所以原点的它们其中的一个公共点,将原点
轴对称的图形,它们有三个公共点,所以原点的它们其中的一个公共点,将原点![]() 代入
代入![]() 中得:
中得:![]() (舍去
(舍去![]() ),此时,曲线
),此时,曲线![]() 方程为
方程为![]() ,曲线
,曲线![]() 和曲线
和曲线![]() 的三个交点坐标为
的三个交点坐标为![]() ,易得这三个点为顶点的三角形的面积为
,易得这三个点为顶点的三角形的面积为![]() .
.
点睛: 参数方程主要通过代入法或者已知恒等式(如![]() 等三角恒等式)消去参数化为普通方程,通过选取相应的参数可以把普通方程化为参数方程,利用关系式
等三角恒等式)消去参数化为普通方程,通过选取相应的参数可以把普通方程化为参数方程,利用关系式![]() ,
, 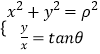 等可以把极坐标方程与直角坐标方程互化,本题这类问题一般我们可以先把曲线方程化为直角坐标方程,用直角坐标方程解决相应问题.
等可以把极坐标方程与直角坐标方程互化,本题这类问题一般我们可以先把曲线方程化为直角坐标方程,用直角坐标方程解决相应问题.

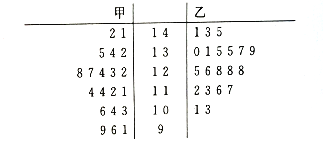
【题目】气象部门提供了某地区今年六月分(30天)的日最高气温的统计表如下:
日最高气温t(单位: |
|
|
|
|
天数 | 6 | 12 |
|
|
由于工作疏忽,统计表被墨水污染,![]() 和
和![]() 数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于
数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于![]() 的频率为0.9.
的频率为0.9.
(1)若把频率看作概率,求![]() ,
,![]() 的值;
的值;
(2)把日最高气温高干![]() 称为本地区的“高温天气”,根据已知条件完成下面2×2列联表,并据此推测是否有95%的把握认为本地区“高温天气”与西瓜“旺销”有关?说明理由.
称为本地区的“高温天气”,根据已知条件完成下面2×2列联表,并据此推测是否有95%的把握认为本地区“高温天气”与西瓜“旺销”有关?说明理由.
高温天气 | 非高温天气 | 合计 | |
旺销 | 1 | ||
不旺销 | 6 | ||
合计 |
附![]()
P(K2≥R) | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
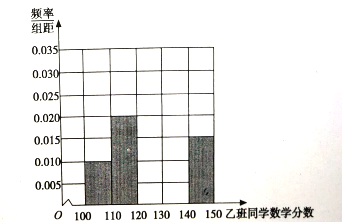
【题目】某市为节约用水,计划在本市试行居民生活用水定额管理,为了较为合理地确定居民日常用水量的标准,通过抽样获得了100位居民某年的月均用水量(单位:吨),右表是100位居民月均用水量的频率分布表,根据右表解答下列问题:
分组 | 频数 | 频率 |
[0,1) | 10 | 0.10 |
[1,2) |
| 0.20 |
[2,3) | 30 | 0.30 |
[3,4) | 20 |
|
[4,5) | 10 | 0.10 |
[5,6] | 10 | 0.10 |
合计 | 100 | 1.00 |

(1)求右表中![]() 和
和![]() 的值;
的值;
(2)请将频率分布直方图补充完整,并根据直方图估计该市每位居民月均用水量的众数.