题目内容
(本小题15分)
已知函数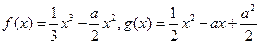 。
。
(I)当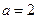 时,求曲线
时,求曲线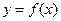 在点
在点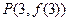 处的切线方程;
处的切线方程;
(Ⅱ)当函数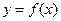 在区间
在区间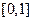 上的最小值为
上的最小值为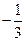 时,求实数
时,求实数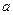 的值;
的值;
(Ⅲ)若函数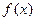 与
与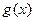 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数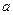 的取值范围。
的取值范围。
(I)因为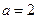 ,由题意
,由题意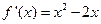 (2分)
(2分) 即过点
即过点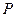 的切线斜率为3,又点
的切线斜率为3,又点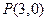
则过点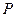 的切线方程为:
的切线方程为: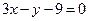 (5分)
(5分)
(Ⅱ)右题意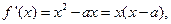 令
令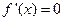 得
得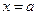 或
或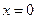 (6分)
(6分)
由 ,要使函数
,要使函数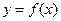 在区间
在区间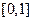 上的最小值为
上的最小值为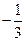 ,则
,则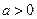
(i)当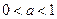 时,
时,
当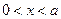 时,
时, ,当
,当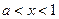 时,
时,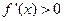 ,
,
所以函数
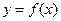 在区间[0,1]上,
在区间[0,1]上,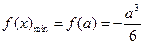
即: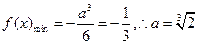 ,舍去 (8分)
,舍去 (8分)
(ii)当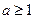 时,
时,
当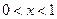 时,
时, ,则使函数
,则使函数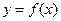 在区间
在区间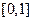 上单调递减,
上单调递减,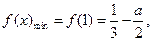
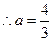
综上所述: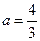 (10分)
(10分)
(Ⅲ)设

令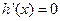 得
得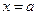 或
或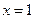 (11分)
(11分)
(i)当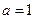 时,函数
时,函数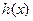 单调递增,函数
单调递增,函数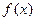 与
与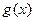 的图象不可能有三个不同的交点
的图象不可能有三个不同的交点
(ii)当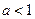 时,
时,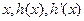 随
随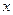 的变化情况如下表:
的变化情况如下表: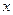
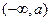
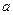
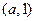
1 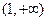
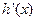
+ 0 一 解析
 练习册系列答案
练习册系列答案
1加1阅读好卷系列答案
专项复习训练系列答案
初中语文教与学阅读系列答案

完形填空与阅读理解周秘计划系列答案
英语阅读理解150篇系列答案
奔腾英语系列答案
标准阅读系列答案
53English系列答案
考纲强化阅读系列答案
相关题目
 (
(
 在
在 处有极值为
处有极值为 ,求
,求 的值;
的值; ,
, 上单调递增,求
上单调递增,求 ,
, 是实数,方程
是实数,方程 有两个实根
有两个实根 ,
, ,数列
,数列 满足
满足 ,
, ,
,
 ,
, ,求
,求 项和.
项和. ,过点
,过点 的直线
的直线 交抛物线
交抛物线 于
于 两点,且
两点,且 .
. 作
作 轴的平行线与直线
轴的平行线与直线 相交于点
相交于点 ,若
,若 是等腰三角形,求直线
是等腰三角形,求直线 的方程.
的方程. 时,不等式f(x)<m恒成立,求实数m的值;
时,不等式f(x)<m恒成立,求实数m的值;