题目内容
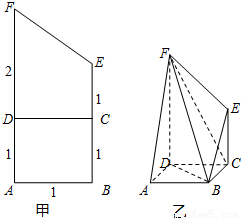
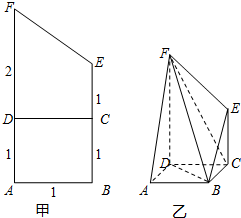 将(如图甲)直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连接部分线段后围成一个空间几何体,如图乙所示.
将(如图甲)直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连接部分线段后围成一个空间几何体,如图乙所示.(1)求异面直线BD与EF所成角的大小;
(2)求二面角D-BF-E的大小.
(3)若F、A、B、C、D这五个点在同一个球面上,求该球的表面积.
分析:先建立空间直角坐标系(1)求出两条异面直线的方向向量的夹角,进而即可异面直线的夹角;
(2)先求出两个平面的法向量的夹角,进而即可求出二面角的大小;
(3)取BF的中点H,可证明H点即为球心,进而可计算出表面积.
(2)先求出两个平面的法向量的夹角,进而即可求出二面角的大小;
(3)取BF的中点H,可证明H点即为球心,进而可计算出表面积.
解答:解:∵平面ABCD⊥平面DCEF,ABCD为正方形,DCEF为直角梯形,
∴分别以DA、DC、DF所在直线为x轴、y轴、z轴建立空间直角坐标系D-xyz,则A(1,0,0),B(1,1,0),C(0,1,0),E(0,1,1),F(0,0,2).
(1)∵
=(1,1,0),
=(0,-1,1),∴cos<
,
>=
=-
,∴<
,
>=
,
∴异面直线BD与EF所成的角为
.
(2)∵AC⊥BD,AC⊥DF,∴AC⊥平面BDF,
∴平面BDF的法向量为
=
=(-1,1,0),
又设平面BEF的一个法向量为
=(1,y,z),而
=(-1,0,1),
=(0,-1,1).
则由
⇒
,
得y=z=1.∴
=(1,1,1).
∵cos<
,
>=
=
=0
∴二面角D-BF-E的大小为90°.
(3)设对角线AC与BD相较于点G,取BF的中点H,连接GH,DH,由直角三角形BDF、ABF、BCF,则HD=HF=HB=HA=HC,
∴H即为球心,且HD=
=
.
∴S球=4π(
)2=6π.
∴分别以DA、DC、DF所在直线为x轴、y轴、z轴建立空间直角坐标系D-xyz,则A(1,0,0),B(1,1,0),C(0,1,0),E(0,1,1),F(0,0,2).
(1)∵
| DB |
| EF |
| DB |
| EF |
| ||||
|
|
| 1 |
| 2 |
| DB |
| EF |
| 2π |
| 3 |
∴异面直线BD与EF所成的角为
| π |
| 3 |
(2)∵AC⊥BD,AC⊥DF,∴AC⊥平面BDF,
∴平面BDF的法向量为
| k |
| AC |

又设平面BEF的一个法向量为
| n |
| BE |
| EF |
则由
|
|
得y=z=1.∴
| n |
∵cos<
| k |
| n |
| ||||
|
|
| 0 | ||||
|
∴二面角D-BF-E的大小为90°.
(3)设对角线AC与BD相较于点G,取BF的中点H,连接GH,DH,由直角三角形BDF、ABF、BCF,则HD=HF=HB=HA=HC,
∴H即为球心,且HD=
| 1 |
| 2 |
22+(
|
| ||
| 2 |
∴S球=4π(
| ||
| 2 |
点评:熟练掌握:通过建立空间直角坐标系利用两条异面直线的方向向量的夹角求异面直线的夹角、利用两个平面的法向量的夹角求二面角及正确找出球心是解题的关键.

练习册系列答案
相关题目
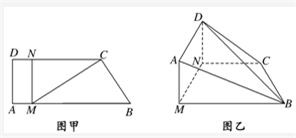 如图甲,直角梯形ABCD中,AB∥CD,∠DAB=
如图甲,直角梯形ABCD中,AB∥CD,∠DAB=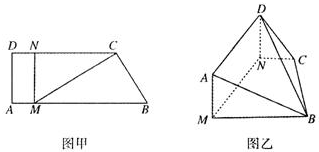 (2009•湖北模拟)如图甲,直角梯形ABCD中,AB∥CD,∠DAB=
(2009•湖北模拟)如图甲,直角梯形ABCD中,AB∥CD,∠DAB=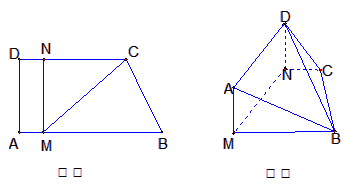 如图甲,直角梯形
如图甲,直角梯形