题目内容
当函数f(x)满足“对于区间(1,2)上的任意x1、x2,有|f(x1)-f(x2)|≤|x1-x2|恒成立,”则称f(x)为优美函数,若f(x)= ,是优美函数,则a的取值范围为
,是优美函数,则a的取值范围为
- A.[-1,1]
- B.(-1,1 )
- C.[0,1]
- D.[0,1)
A
分析:由于x1<x2时总有f(x2)-f(x1)>x2-x1成立,故可将解析式代入,进行整理化简,分离出常数a来,得到关于a在区间(1,2)上恒成立进而判断出右边式子的最值,得出参数a的取值范围.
解答:∵|f(x1)-f(x2)|>|x1-x2|
∴| |≤|x1-x2|
|≤|x1-x2|
∴
∴|a|≤x1x2在x∈(1,2)上恒成立
∵1<x1x2<4
∴|a|≤1
∴-1≤a≤1
故选A
点评:本题考点是函数恒成立的问题,通过对|f(x2)-f(x1)|>|x2-x1|转化变形,得到关于参数的不等式在区间(1,2)上恒成立,此种方法是分离常数法在解题中的应用,对此类恒成立求参数的问题,要注意此类技巧的使用.
分析:由于x1<x2时总有f(x2)-f(x1)>x2-x1成立,故可将解析式代入,进行整理化简,分离出常数a来,得到关于a在区间(1,2)上恒成立进而判断出右边式子的最值,得出参数a的取值范围.
解答:∵|f(x1)-f(x2)|>|x1-x2|
∴|
 |≤|x1-x2|
|≤|x1-x2|∴

∴|a|≤x1x2在x∈(1,2)上恒成立
∵1<x1x2<4
∴|a|≤1
∴-1≤a≤1
故选A
点评:本题考点是函数恒成立的问题,通过对|f(x2)-f(x1)|>|x2-x1|转化变形,得到关于参数的不等式在区间(1,2)上恒成立,此种方法是分离常数法在解题中的应用,对此类恒成立求参数的问题,要注意此类技巧的使用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
定义域为R的函数f(x)满足f(x+1)=2f(x),且当x∈(0,1]时,f(x)=x2-x,则当x∈[-2,-1]时,f(x)的最小值为( )
A、-
| ||
B、-
| ||
C、-
| ||
| D、0 |
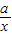 ,是优美函数,则a的取值范围为( )
,是优美函数,则a的取值范围为( )