题目内容
8．高为2的圆柱侧面积为4π，此圆柱的体积为2π．分析 根据已知求出圆锥的底面半径，代入圆柱体积公式，可得答案．
解答 解：设圆柱的底面半径为r，
∵圆柱侧面积为4π=2πr×2，
∴r=1，
故圆柱的体积V=π•12•2=2π，
故答案为：2π．
点评 本题考查的知识点是圆柱的表面积和体积，其中根据已知条件，求出圆柱的底面半径，是解答本题的关键．
练习册系列答案
相关题目
19．如果f（x）=$\frac{1}{2}$（m-2）x2+（n-8）x+1（m＞2，n＞0）在[$\frac{1}{2}，2$]上单调递减，则$\frac{1}{m}$+$\frac{1}{n}$的最小值为（ ）
| A． | $\frac{\sqrt{2}}{3}$ | B． | $\frac{\sqrt{2}}{6}$ | C． | $\frac{3+2\sqrt{2}}{12}$ | D． | $\frac{3-2\sqrt{2}}{12}$ |
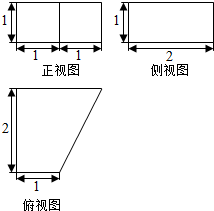一个几何体的三视图如图所示：
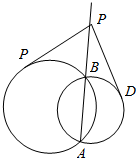如图，两圆相交于A、B两点，P为两圆公共弦AB上任一点，从P引两圆的切线PC、PD，若PC=2$\sqrt{2}$cm，则PD=2$\sqrt{2}$cm．
18．f（x）=ax2+bx+c满足f（0）=3，对称轴是直线x=-1，最小值为2，则该函数的表达式为（ ）
| A． | f（x）=x2-2x-3 | B． | f（x）=x2+2x-3 | C． | f（x）=x2-2x+3 | D． | f（x）=x2+2x+3 |