题目内容
(2012•海淀区一模)已知函数f(x)=
则
(ⅰ)f(f(x))=
(ⅱ)给出下列三个命题:
①函数f(x)是偶函数;
②存在xi∈R(i=1,2,3),使得以点(xi,f(xi))(i=1,2,3)为顶点的三角形是等腰直角三角形;
③存在xi∈R(i=1,2,3,4),使得以点(xi,f(xi))(i=1,2,3,4)为顶点的四边形为菱形.
其中,所有真命题的序号是
|
(ⅰ)f(f(x))=
1
1
;(ⅱ)给出下列三个命题:
①函数f(x)是偶函数;
②存在xi∈R(i=1,2,3),使得以点(xi,f(xi))(i=1,2,3)为顶点的三角形是等腰直角三角形;
③存在xi∈R(i=1,2,3,4),使得以点(xi,f(xi))(i=1,2,3,4)为顶点的四边形为菱形.
其中,所有真命题的序号是
①③
①③
.分析:(ⅰ)对x分类:x∈Q和x∈
,再由解析式求出f(f(x))的值;
(ⅱ)①对x分类:x∈Q和x∈
,分别判断出f(-x)=f(x),再由偶函数的定义判断出①正确;
②由解析式做出大致图象:根据图象和等腰直角三角形的性质,进行判断即可;
③取两个自变量是有理数,使得另外两个无理数差与两个有理数的差相等,即可得出此四边形为平行四边形.
| C | Q R |
(ⅱ)①对x分类:x∈Q和x∈
| C | Q R |
②由解析式做出大致图象:根据图象和等腰直角三角形的性质,进行判断即可;
③取两个自变量是有理数,使得另外两个无理数差与两个有理数的差相等,即可得出此四边形为平行四边形.
解答:解:(ⅰ)由题意知,f(x)=
,
当x∈Q时,f(x)=1∈Q,则f(f(x))=1,
当x∈
时,f(x)=0∈Q,则f(f(x))=1,
综上得,f(f(x))=1;
(ⅱ)①当x∈Q时,则-x∈Q,故f(-x)=1=f(x),
当x∈
时,则-x∈
,故f(-x)=0=f(x),
∴函数f(x)是偶函数,①正确;
②根据f(x)=
,做出函数的大致图象:
假设存在等腰直角三角形ABC,则斜边AB只能在x轴上或在直线y=1上,且斜边上的高始终是1,不妨假设A,B在x轴上,如图
故斜边AB=2,故点A、B的坐标不可能是无理数,否则O点不再是中点,故不存在
另外,当AB在y=1上,C在x轴时,由于AB=2,则C的坐标应是有理数,
故假设不成立,即不存在符合题意的等腰直角三角形,②错误;
③根据②做出的图形知,
取两个自变量是有理数,使得另外两个无理数差与两个有理数的差相等,即可画出平行四边形,且是对角线相互垂直,
可以做出以点(xi,f(xi))(i=1,2,3,4)为顶点的四边形为菱形,③正确.
故答案为:1,①③.
|
当x∈Q时,f(x)=1∈Q,则f(f(x))=1,
当x∈
| C | Q R |

综上得,f(f(x))=1;
(ⅱ)①当x∈Q时,则-x∈Q,故f(-x)=1=f(x),
当x∈
| C | Q R |
| C | Q R |
∴函数f(x)是偶函数,①正确;
②根据f(x)=
|
假设存在等腰直角三角形ABC,则斜边AB只能在x轴上或在直线y=1上,且斜边上的高始终是1,不妨假设A,B在x轴上,如图
故斜边AB=2,故点A、B的坐标不可能是无理数,否则O点不再是中点,故不存在
另外,当AB在y=1上,C在x轴时,由于AB=2,则C的坐标应是有理数,
故假设不成立,即不存在符合题意的等腰直角三角形,②错误;
③根据②做出的图形知,
取两个自变量是有理数,使得另外两个无理数差与两个有理数的差相等,即可画出平行四边形,且是对角线相互垂直,
可以做出以点(xi,f(xi))(i=1,2,3,4)为顶点的四边形为菱形,③正确.
故答案为:1,①③.
点评:本题考查了分段函数的求值,奇偶性的判断,以及数形结合思想和分类讨论的应用,难度较大.

练习册系列答案
相关题目
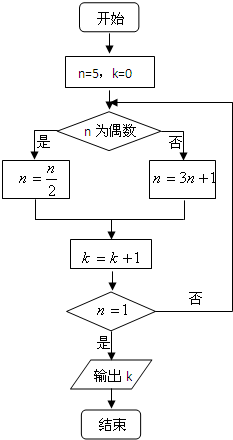 (2012•海淀区一模)执行如图所示的程序框图,输出的k值是( )
(2012•海淀区一模)执行如图所示的程序框图,输出的k值是( )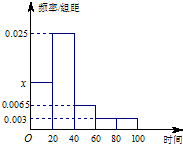 (2012•海淀区一模)某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
(2012•海淀区一模)某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].