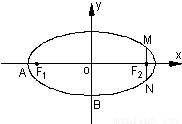
题目内容
设椭圆C: 的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且
的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且 .
.(1)求椭圆C的离心率;
(2)若过A、Q、F2三点的圆恰好与直线l:
 相切,求椭圆C的方程;
相切,求椭圆C的方程;(3)在(2)的条件下,过右焦点F2作斜率为k的直线l与椭圆C交于M、N两点,在x轴上是否存在点P(m,0)使得以PM,PN为邻边的平行四边形是菱形,如果存在,求出m的取值范围,如果不存在,说明理由.
.

【答案】分析:(1)设Q(x,0),由F2(c,0),A(0,b)结合向量条件及向量运算得出关于a,c的等式,从而求得椭圆的离心率即可;
(2)由(1)知a,c的一个方程,再利用△AQF的外接圆得出另一个方程,解这两个方程组成的方程组即可求得所求椭圆方程;
(3)由(Ⅱ)知直线l:y=k(x-1),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得满足题意的点P且m的取值范围.
解答:解:(1)设Q(x,0),由F2(c,0),A(0,b)
知
∵ ,∴
,∴ ,
,
由于 即F1为F2Q中点.
即F1为F2Q中点.
故 ∴b2=3c2=a2-c2,
∴b2=3c2=a2-c2,
故椭圆的离心率 ,(3分)
,(3分)
(2)由(1)知 ,得
,得 于是F2(
于是F2( a,0)Q
a,0)Q ,
,
△AQF的外接圆圆心为(- a,0),半径r=
a,0),半径r= |FQ|=a
|FQ|=a
所以 ,解得a=2,∴c=1,b=
,解得a=2,∴c=1,b= ,
,
所求椭圆方程为 ,(6分)
,(6分)
(3)由(Ⅱ)知F2(1,0)l:y=k(x-1)
代入得(3+4k2)x2-8k2x+4k2-12=0
设M(x1,y1),N(x2,y2)
则 ,y1+y2=k(x1+x2-2),(8分)
,y1+y2=k(x1+x2-2),(8分)
 =(x1+x2-2m,y1+y2)
=(x1+x2-2m,y1+y2)
由于菱形对角线垂直,则

故k(y1+y2)+x1+x2-2m=0
则k2(x1+x2-2)+x1+x2-2m=0k2
 (10分)
(10分)
由已知条件知k≠0且k∈R∴ ∴
∴
故存在满足题意的点P且m的取值范围是 .(12分)
.(12分)
点评:当直线与圆锥曲线相交时 涉及弦长问题,常用“韦达定理法”设而不求计算弦长(即应用弦长公式);涉及弦长的中点问题,常用“点差法”设而不求,将弦所在直线的斜率、弦的中点坐标联系起来,相互转化 同时还应充分挖掘题目的隐含条件,寻找量与量间的关系灵活转化,往往就能事半功倍.
(2)由(1)知a,c的一个方程,再利用△AQF的外接圆得出另一个方程,解这两个方程组成的方程组即可求得所求椭圆方程;
(3)由(Ⅱ)知直线l:y=k(x-1),将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用弦长公式即可求得满足题意的点P且m的取值范围.
解答:解:(1)设Q(x,0),由F2(c,0),A(0,b)
知

∵
 ,∴
,∴ ,
,由于
 即F1为F2Q中点.
即F1为F2Q中点.故
 ∴b2=3c2=a2-c2,
∴b2=3c2=a2-c2,故椭圆的离心率
 ,(3分)
,(3分)(2)由(1)知
 ,得
,得 于是F2(
于是F2( a,0)Q
a,0)Q ,
,△AQF的外接圆圆心为(-
 a,0),半径r=
a,0),半径r= |FQ|=a
|FQ|=a所以
 ,解得a=2,∴c=1,b=
,解得a=2,∴c=1,b= ,
,所求椭圆方程为
 ,(6分)
,(6分)(3)由(Ⅱ)知F2(1,0)l:y=k(x-1)

代入得(3+4k2)x2-8k2x+4k2-12=0
设M(x1,y1),N(x2,y2)
则
 ,y1+y2=k(x1+x2-2),(8分)
,y1+y2=k(x1+x2-2),(8分) =(x1+x2-2m,y1+y2)
=(x1+x2-2m,y1+y2)由于菱形对角线垂直,则


故k(y1+y2)+x1+x2-2m=0
则k2(x1+x2-2)+x1+x2-2m=0k2

 (10分)
(10分)由已知条件知k≠0且k∈R∴
 ∴
∴
故存在满足题意的点P且m的取值范围是
 .(12分)
.(12分)点评:当直线与圆锥曲线相交时 涉及弦长问题,常用“韦达定理法”设而不求计算弦长(即应用弦长公式);涉及弦长的中点问题,常用“点差法”设而不求,将弦所在直线的斜率、弦的中点坐标联系起来,相互转化 同时还应充分挖掘题目的隐含条件,寻找量与量间的关系灵活转化,往往就能事半功倍.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,在直角坐标系xOy中,已知椭圆C:
如图,在直角坐标系xOy中,已知椭圆C:
 =1(a>b>0)的左、右两个焦 点。(1)若椭圆C上的点A(1,
=1(a>b>0)的左、右两个焦 点。(1)若椭圆C上的点A(1, )到F1、F2两点的 距离之和等于4,写出椭圆C的方程和焦点坐标;
)到F1、F2两点的 距离之和等于4,写出椭圆C的方程和焦点坐标; +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
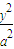 +
+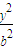 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=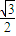 ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的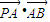 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.