Question

过点B(1,1)能否作直线l,使它与双曲线x²-=1交于Q₁、Q₂两点,且点B是线段Q₁Q₂的中点?如果存在,求出方程;如果不存在,请说明理由.

Answer 1

思路分析:从题设出发,通过解方程组,利用韦达定理,将图形特征转化为数量关系,判断方程组是否有解.

解:假设存在这样的直线l,

方程x=1显然不合题意,

故设l的方程为y-1=k(x-1).

由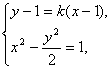

得(2-k²)x²+(2k²-k)x-k²+2k-3=0.                                                (*)

设Q₁(x₁,y₁)、Q₂(x₂,y₂),则由Q₁Q₂的中点为B(1,1),

则x₁+x₂=2.

∴x₁+x₂==2.∴k=2.

故直线l的方程为y-1=2(x-1).

当k=2时,(*)式方程可化为-2x²+4x-3=0,

即2x²-4x+3=0,而Δ=16-4×2×3＜0,

∴此直线l不存在.