题目内容
若第二象限的角α满足tanα=-
,则cosα= .
| 1 | 3 |
分析:由α为第二象限角,得到cosα小于0,利用同角三角函数间的倒数关系cosα=
及sec2α=tan2α+1把所求的式子化简后,将tanα的值代入即可求出值.
| 1 |
| secα |
解答:解:∵第二象限的角α满足tanα=-
,
∴cosα=
=-
=-
.
故答案为:-
| 1 |
| 3 |
∴cosα=
| 1 |
| secα |
| 1 | ||
|
3
| ||
| 10 |
故答案为:-
3
| ||
| 10 |
点评:此题考查了同角三角函数间基本关系的应用,熟练掌握基本关系是解本题的关键,同时注意角度的范围.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 所在的象限,并用图形表示其变化范围.
所在的象限,并用图形表示其变化范围. ,则cosα=________.
,则cosα=________.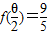 ,求
,求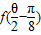 的值.
的值.