题目内容
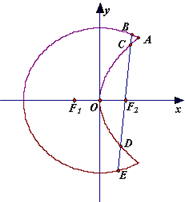 如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|=
如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|=| 7 |
| 2 |
| 5 |
| 2 |
(1)求曲线C1和C2的方程;
(2)过F2作一条与x轴不垂直的直线,分别与曲线C1、C2依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
| |BE|•|GF2| |
| |CD|•|HF2| |
分析:(1)因为在椭圆中2a=|AF1|+|AF2|=
+
=6,所以可求曲线C1方程.,因为曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点.|AF1|=
,|AF2|=
,所以利用抛物线定义,可求,曲线C2方程.
(2)先设出B、C、D、E四点坐标,过F2作的与x轴不垂直的直线方程,在分别与椭圆方程,抛物线方程联立,利用根与系数关系,求
的值,看结果是否为定值.
| 7 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
| 5 |
| 2 |
(2)先设出B、C、D、E四点坐标,过F2作的与x轴不垂直的直线方程,在分别与椭圆方程,抛物线方程联立,利用根与系数关系,求
| |BE|•|GF2| |
| |CD|•|HF2| |
解答:解:(1)设椭圆方程为
+
= 1,则2a=|AF1|+|AF2|=
+
=6,得a=3
设A(x,y),F1(-c,0),F2(c,0∵|AF1|=
,|AF2|=
则(x+c)2+y2=(
)2
(x-c)2+y2=(
)2,两式相减得xc=
,由抛物线定义可知,|AF2|=x+c=
则c=1,x=
或x=1,c=
(舍去)
所以椭圆方程为
+
= 1 抛物线方程为y2=4x
(2)设B(x1,y1),E(x2,y2),C(x3,y3),D(x4,y4),
设过F2作一条与x轴不垂直的直线方程为y=k(x-1),代入
+
= 1,
得(8+9k2)y2+16ky-64k2=0
∴y1+y2=-
,y1y2=
同理,把y=k(x-1)代入y2=4x,得,ky2-4y-4k=0,y3+y4=
,y3y4=-4
所以
=
•
=
=
=
=3
| x2 |
| a2 |
| y2 |
| b2 |
| 7 |
| 2 |
| 5 |
| 2 |
设A(x,y),F1(-c,0),F2(c,0∵|AF1|=
| 7 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
(x-c)2+y2=(
| 5 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
则c=1,x=
| 3 |
| 2 |
| 3 |
| 2 |
所以椭圆方程为
| x2 |
| 9 |
| y2 |
| 8 |
(2)设B(x1,y1),E(x2,y2),C(x3,y3),D(x4,y4),
设过F2作一条与x轴不垂直的直线方程为y=k(x-1),代入
| x2 |
| 9 |
| y2 |
| 8 |
得(8+9k2)y2+16ky-64k2=0
∴y1+y2=-
| 16k |
| 8+9k2 |
| 64k2 |
| 8+9k2 |
同理,把y=k(x-1)代入y2=4x,得,ky2-4y-4k=0,y3+y4=
| 4 |
| k |
所以
| |BE|•|GF2| |
| |CD|•|HF2| |
| |y1-y2| |
| |y3-y4| |
| ||
|
|
=
|
|
点评:本题考察了椭圆,抛物线与直线的位置关系,掌握设而不求思想的应用.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
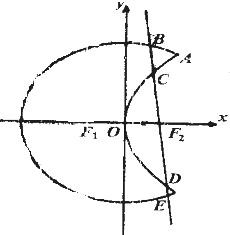 曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点,F2(1,0)为焦点的抛物线的一部分,
曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点,F2(1,0)为焦点的抛物线的一部分,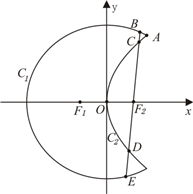 如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点,曲线C1的离心率为
如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点,曲线C1的离心率为 (2012•孝感模拟)如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|=
(2012•孝感模拟)如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|= 如图,曲线C1是以原点O为中心,F1、F2为焦点的椭圆的一部分,曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分,
如图,曲线C1是以原点O为中心,F1、F2为焦点的椭圆的一部分,曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分,