题目内容
 (2012•孝感模拟)如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|=
(2012•孝感模拟)如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|=| 7 |
| 2 |
| 5 |
| 2 |
(I)求曲线C1和C2的方程;
(II)设点C是C2上一点,若|CF1|=
| 2 |
分析:(I)设曲线C1的方程为
+
=1(a>b>0),则根据|AF1|=
,|AF2|=
,可得a=3,设A(x,y),F1(-c,0),F2(c,0),则(x+c)2+y2=
,(x-c)2+y2=
,由此可求曲线C1和C2的方程;
(II)过点F1作直线l垂直于x轴,过点C作直线CC1⊥l于点C1,依题意知l为抛物线C2的准线,则|CC1|=|CF2|,在△CF1F2中,设|CF2|=r,则|CF1|=
r,|F1F2|=2,由余弦定理可得r=2,再利用三角形的面积公式,即可求得结论.
| x2 |
| a2 |
| y2 |
| b2 |
| 7 |
| 2 |
| 5 |
| 2 |
| 49 |
| 4 |
| 25 |
| 4 |
(II)过点F1作直线l垂直于x轴,过点C作直线CC1⊥l于点C1,依题意知l为抛物线C2的准线,则|CC1|=|CF2|,在△CF1F2中,设|CF2|=r,则|CF1|=
| 2 |
解答:解:(I)设曲线C1的方程为
+
=1(a>b>0),则2a=|AF1|+|AF2|=
+
=6得a=3
设A(x,y),F1(-c,0),F2(c,0),则(x+c)2+y2=
,(x-c)2+y2=
两式相减可得:xc=
由抛物线定义可知|AF2|=x+c=
∴c=1,x=
或x=1,c=
(舍去)
所以曲线C1的方程为
+
=1(-3≤x≤
),C2的方程为y2=4x(0≤x≤
);
(II)过点F1作直线l垂直于x轴,过点C作直线CC1⊥l于点C1,依题意知l为抛物线C2的准线,则|CC1|=|CF2|
在直角△CC1F1中,|CF1|=
|CC1|,∠C1CF1=45°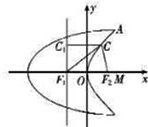
∵∠CF1F2=∠C1CF1=45°
在△CF1F2中,设|CF2|=r,则|CF1|=
r,|F1F2|=2
由余弦定理可得22+2r2-2×2×
rcos45°=r2,
∴r=2
∴S△CF1F2=
×2×2
sin45°=2
| x2 |
| a2 |
| y2 |
| b2 |
| 7 |
| 2 |
| 5 |
| 2 |
设A(x,y),F1(-c,0),F2(c,0),则(x+c)2+y2=
| 49 |
| 4 |
| 25 |
| 4 |
两式相减可得:xc=
| 3 |
| 2 |
由抛物线定义可知|AF2|=x+c=
| 5 |
| 2 |
∴c=1,x=
| 3 |
| 2 |
| 3 |
| 2 |
所以曲线C1的方程为
| x2 |
| 9 |
| y2 |
| 8 |
| 3 |
| 2 |
| 3 |
| 2 |
(II)过点F1作直线l垂直于x轴,过点C作直线CC1⊥l于点C1,依题意知l为抛物线C2的准线,则|CC1|=|CF2|
在直角△CC1F1中,|CF1|=
| 2 |

∵∠CF1F2=∠C1CF1=45°
在△CF1F2中,设|CF2|=r,则|CF1|=
| 2 |
由余弦定理可得22+2r2-2×2×
| 2 |
∴r=2
∴S△CF1F2=
| 1 |
| 2 |
| 2 |
点评:本题考查了椭圆,抛物线方程的求法,考查三角形面积的计算,求得方程是关键.

练习册系列答案
相关题目
 (2012•孝感模拟)如图,在A、B间有四个焊接点,若焊接点脱落,而可能导致电路不通,如今发现A、B之间线路不通,则焊接点脱落的不同情况有( )
(2012•孝感模拟)如图,在A、B间有四个焊接点,若焊接点脱落,而可能导致电路不通,如今发现A、B之间线路不通,则焊接点脱落的不同情况有( )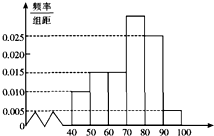 (2012•孝感模拟)某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如右图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
(2012•孝感模拟)某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如右图所示的部分频率分布直方图,请观察图形信息,回答下列问题: