题目内容
在 中,角
中,角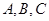 所对的边分别为
所对的边分别为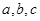 且满足
且满足 .
.
(I)求角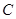 的大小;
的大小;
(II)求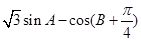 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角 的大小.
的大小.
(I)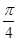 ;(II)最大值为2,此时
;(II)最大值为2,此时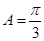 ,
,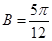 .
.
解析试题分析:(I)由正弦定理将 转化为角的关系,再利用三角函数关系式解答,在三角形中求角或边,通常对条件进行“统一”,统一为边或统一为角,主要的工具是正弦定理和余弦定理,同时不要忘记了三角形内角和定理;(II)先通过三角函数的恒等变形化
转化为角的关系,再利用三角函数关系式解答,在三角形中求角或边,通常对条件进行“统一”,统一为边或统一为角,主要的工具是正弦定理和余弦定理,同时不要忘记了三角形内角和定理;(II)先通过三角函数的恒等变形化 的形式后再解答,一般地,涉及三角函数的值域问题,多数情况下要将其变形为
的形式后再解答,一般地,涉及三角函数的值域问题,多数情况下要将其变形为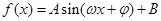 后,再利用三角函数的性质解答,也有部分题目,可转化为角的某个三角函数,然后用换元法转化为非三角函数问题.
后,再利用三角函数的性质解答,也有部分题目,可转化为角的某个三角函数,然后用换元法转化为非三角函数问题.
试题解析:(I)由正弦定理得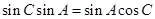 ,因为
,因为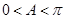 所以
所以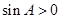 ,从而
,从而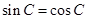 ,又
,又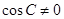 ,所以
,所以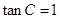 ,则
,则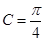 5分
5分
(II)由(I)知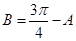 , 6分
, 6分
于是 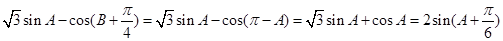 ,
,
因为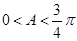 ,所以
,所以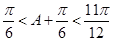 ,从而当
,从而当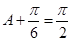 ,即
,即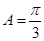 时,
时, 取最大值2.
取最大值2.
综上所述,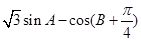 的最大值为2,此时
的最大值为2,此时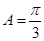 ,
,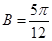 13分
13分
考点:三角函数性质、正弦定理.

练习册系列答案
相关题目
 ,
,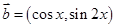 ,
,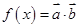 .(1)求
.(1)求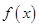 的最小正周期、最大值及
的最小正周期、最大值及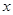 的集合;
的集合;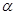 满足
满足 ,求
,求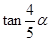 的值.
的值.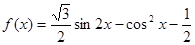 ,
,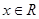 .
.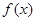 的最小值和最小正周期;
的最小值和最小正周期;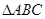 的内角
的内角 、
、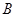 、
、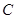 的对边分别为
的对边分别为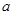 、
、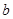 、
、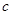 ,满足
,满足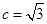 ,
,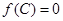 且
且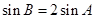 ,求
,求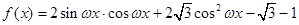 (其中
(其中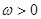 ),
),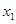 、
、 是函数
是函数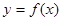 的两个不同的零点,且
的两个不同的零点,且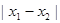 的最小值为
的最小值为 .
. 的值;
的值;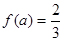 ,求
,求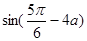 的值.
的值.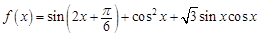 .
.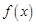 最大值和最小正周期;
最大值和最小正周期;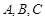 为
为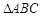 的三个内角,若
的三个内角,若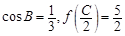 ,求
,求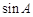 .
.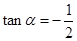 ,求
,求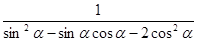 的值;
的值;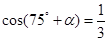 ,且
,且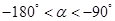 ,求
,求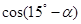 的值.
的值.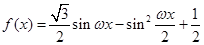 (
(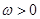 )的最小正周期为
)的最小正周期为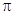 .
.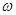 的值及函数
的值及函数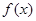 的单调递增区间;
的单调递增区间;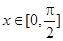 时,求函数
时,求函数 .
.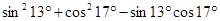 ;
;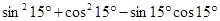 ;
; 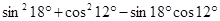 ;
;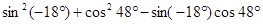 ;
;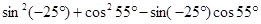 .
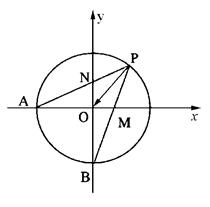
.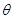 的直线
的直线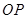 与单位圆在第一象限的部分交于点
与单位圆在第一象限的部分交于点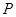 ,单位圆与坐标轴交于点
,单位圆与坐标轴交于点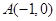 ,点
,点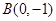 ,
,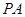 与
与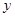 轴交于点
轴交于点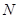 ,
, 与
与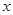 轴交于点
轴交于点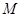 ,设
,设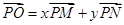
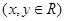
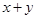 的最小值.
的最小值.