Question

已知圆C的圆心为原点O，且与直线x+y+4

2

=0相切．
（1）求圆C的方程；
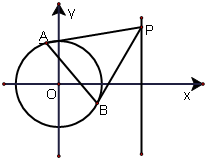
（2）点P在直线x=8上，过P点引圆C的两条切线PA，PB，切点为A，B，求证：直线AB恒过定点．

Answer 1

（本小题满分14分）
（1）依题意得：圆心（0，0）到直线x+y+4

2

=0的距离d=r，
∴d=r=

4 2

1+1

=4，---（2分）
所以圆C的方程为x²+y²=16①；-----（4分）
（2）连接OA，OB，
∵PA，PB是圆C的两条切线，
∴OA⊥AP，OB⊥BP，------（5分）
∴A，B在以OP为直径的圆上，-------（6分）
设点P的坐标为（8，b），b∈R，
则线段OP的中点坐标为(4，

b

2

)，------（8分）
∴以OP为直径的圆方程为(x-4)2+(y-

b

2

)2=42+(

b

2

)2，b∈R，-----（10分）
化简得：x²+y²-8x-by=0②，b∈R，------（11分）
∵AB为两圆的公共弦，
∴①-②得：直线AB的方程为8x+by=16，b∈R，即8（x-2）+by=0，------（13分）
则直线AB恒过定点（2，0）．-------（14分）