题目内容
已知数列{an}的首项a1=4,且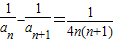 (n∈N*),数列{bn}的前n项和Sn=2-bn.
(n∈N*),数列{bn}的前n项和Sn=2-bn.(1)求数列{an}和{bn}的通项公式;
(2)设
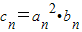 ,证明:当且仅当n≥3时,cn+1<cn.
,证明:当且仅当n≥3时,cn+1<cn.
【答案】分析:(1)由已知中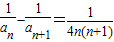 ,利用裂项相消法可得
,利用裂项相消法可得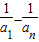 =
=
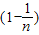 ,结合a1=4,可得数列{an}的通项公式,由数列{bn}的前n项和Sn=2-bn,根据n≥2时,Sn-1=2-bn-1,易得数列为等比数列,求出首项后,可得数列{bn}的通项公式
,结合a1=4,可得数列{an}的通项公式,由数列{bn}的前n项和Sn=2-bn,根据n≥2时,Sn-1=2-bn-1,易得数列为等比数列,求出首项后,可得数列{bn}的通项公式
(2)由(1)中数列{an}和{bn}的通项公式;求出数列{Cn}的通项公式,作差Cn+1-Cn并化简,易得当n<3时,Cn+1-Cn>0,当n≥3时,Cn+1-Cn<0,综合讨论结果,可得答案.
解答:解:(1)∵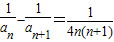 =
=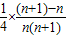 =
=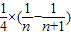
∴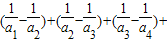 …
…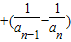 =
=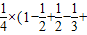 …
…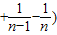 =
=
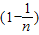
即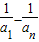 =
=
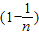
又∵a1=4,
∴an=4n,
∵数列{bn}的前n项和Sn=2-bn…①
当n≥2时,Sn-1=2-bn-1…②
①-②得bn=bn-1-bn,
即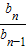 =
=
又∵n=1时,S1=2-b1=b1,
∴b1=1
故数列{bn}是一个以1为首项,以 为公比的等比数列
为公比的等比数列
故bn=21-n
证明:(2)∵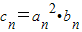 =n225-n
=n225-n
∴Cn+1-Cn=(n+1)224-n-n225-n=24-n[-(n-1)2+2]
当n<3时,Cn+1-Cn>0
当n≥3时,Cn+1-Cn<0
即当且仅当n≥3时,cn+1<cn.
点评:本题考查的知识点是数列与不等式的综合,数列的递推式,(1)的关键是熟练掌握求数列通项公式的方法,(2)的关键是作差Cn+1-Cn并化简.
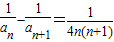 ,利用裂项相消法可得
,利用裂项相消法可得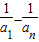 =
=
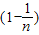 ,结合a1=4,可得数列{an}的通项公式,由数列{bn}的前n项和Sn=2-bn,根据n≥2时,Sn-1=2-bn-1,易得数列为等比数列,求出首项后,可得数列{bn}的通项公式
,结合a1=4,可得数列{an}的通项公式,由数列{bn}的前n项和Sn=2-bn,根据n≥2时,Sn-1=2-bn-1,易得数列为等比数列,求出首项后,可得数列{bn}的通项公式(2)由(1)中数列{an}和{bn}的通项公式;求出数列{Cn}的通项公式,作差Cn+1-Cn并化简,易得当n<3时,Cn+1-Cn>0,当n≥3时,Cn+1-Cn<0,综合讨论结果,可得答案.
解答:解:(1)∵
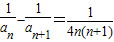 =
=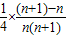 =
=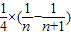
∴
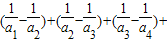 …
…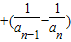 =
=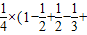 …
…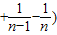 =
=
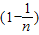
即
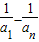 =
=
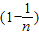
又∵a1=4,
∴an=4n,
∵数列{bn}的前n项和Sn=2-bn…①
当n≥2时,Sn-1=2-bn-1…②
①-②得bn=bn-1-bn,
即
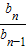 =
=
又∵n=1时,S1=2-b1=b1,
∴b1=1
故数列{bn}是一个以1为首项,以
 为公比的等比数列
为公比的等比数列故bn=21-n
证明:(2)∵
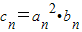 =n225-n
=n225-n∴Cn+1-Cn=(n+1)224-n-n225-n=24-n[-(n-1)2+2]
当n<3时,Cn+1-Cn>0
当n≥3时,Cn+1-Cn<0
即当且仅当n≥3时,cn+1<cn.
点评:本题考查的知识点是数列与不等式的综合,数列的递推式,(1)的关键是熟练掌握求数列通项公式的方法,(2)的关键是作差Cn+1-Cn并化简.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目