题目内容
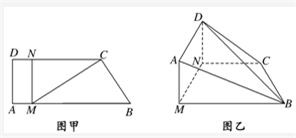
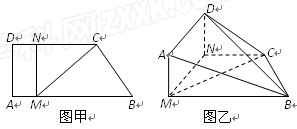
如图甲,直角梯形ABCD中,AB∥CD,∠DAB= ,点M、N分别在AB,CD上,且MN⊥AB,MC⊥CB,BC=2,MB=4,现将梯形ABCD沿MN折起,使平面AMND与平面MNCB垂直(如图乙),
,点M、N分别在AB,CD上,且MN⊥AB,MC⊥CB,BC=2,MB=4,现将梯形ABCD沿MN折起,使平面AMND与平面MNCB垂直(如图乙),
(Ⅰ)求证:AB∥平面DNC;
(Ⅱ)当DN的长为何值时,二面角D-BC-N的大小为30°?
 ,点M、N分别在AB,CD上,且MN⊥AB,MC⊥CB,BC=2,MB=4,现将梯形ABCD沿MN折起,使平面AMND与平面MNCB垂直(如图乙),
,点M、N分别在AB,CD上,且MN⊥AB,MC⊥CB,BC=2,MB=4,现将梯形ABCD沿MN折起,使平面AMND与平面MNCB垂直(如图乙),(Ⅰ)求证:AB∥平面DNC;
(Ⅱ)当DN的长为何值时,二面角D-BC-N的大小为30°?

解:(Ⅰ)MB∥NC,MB 平面DNC,NC 平面DNC,NC 平面DNC, 平面DNC,∴MB∥平面DNC, 同理MA∥平面DNC, 又MA∩MB=M,且MA,MB  平面MAB, 平面MAB, ∴  。 。 |
|
| (Ⅱ)过N作NH⊥BC交BC延长线于H,连结HN, ∵平面AMND⊥平面MNCB,DN⊥MN, ∴DN⊥平面MBCN,从而DH⊥BC, ∴∠DHN为二面角D-BC-N的平面角, ∴∠DHN=30°, 由MB=4,BC=2,∠MCB=90°知∠MBC=60°,  , , ∴NH=3·sin60°=  , ,由条件知:  , ,∴  。 。 |
 |

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 如图甲,直角梯形ABCD中,AB∥CD,∠DAB=
如图甲,直角梯形ABCD中,AB∥CD,∠DAB=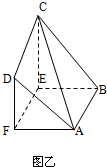
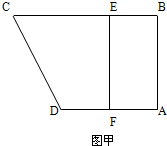 如图甲,直角梯形ABCD中,AB⊥AD,AD∥BC,F为AD的中点,E在BC上,且EF∥AB,已知AB=AD=CE=2,现沿EF把四边形CDFE折起如图乙,使平面CDFE⊥平面ABEF.
如图甲,直角梯形ABCD中,AB⊥AD,AD∥BC,F为AD的中点,E在BC上,且EF∥AB,已知AB=AD=CE=2,现沿EF把四边形CDFE折起如图乙,使平面CDFE⊥平面ABEF.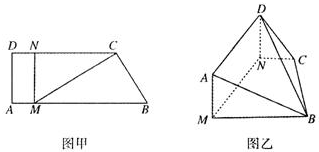 (2009•湖北模拟)如图甲,直角梯形ABCD中,AB∥CD,∠DAB=
(2009•湖北模拟)如图甲,直角梯形ABCD中,AB∥CD,∠DAB=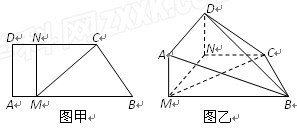
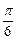 ?
?
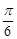 ?
?