题目内容
已知函数 .
.
(1)若 ,则
,则 的定义域为 ;
的定义域为 ;
(2)若 在区间
在区间 上是减函数, 则实数
上是减函数, 则实数 的取值范围是 .
的取值范围是 .
(1)  ;(2)
;(2)
解析试题分析:(1)由 ,求解即可得到
,求解即可得到 ,故
,故 的定义域为
的定义域为 ;(2)当
;(2)当 时,
时, ,
, 在其定义域内单调递减,由复合函数的单调性可知要使
在其定义域内单调递减,由复合函数的单调性可知要使 在区间
在区间 单调递减,须满足
单调递减,须满足 即
即 ,求解得
,求解得 ;当
;当 时,
时, ,由复合函数的单调性可知要使
,由复合函数的单调性可知要使 在区间
在区间 单调递减,则须满足函数
单调递减,则须满足函数 在
在 单调递增且最小值必须大于0,此时
单调递增且最小值必须大于0,此时 ;综上可知,
;综上可知, .
.
考点:1.函数的定义域;2.函数的单调性;3.分类讨论的思想.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
已知函数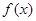 的定义域为
的定义域为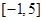 ,部分对应值如下表,
,部分对应值如下表,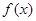 的导函数
的导函数
 ,
,
的图象如图所示.
 | ﹣1 | 0 | 2 | 4 | 5 |
 | 1 | 2 | 0 | 2 | 1 |

(1)
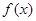 的极小值为 _______;
的极小值为 _______;(2)若函数
 有4个零点,则实数
有4个零点,则实数 的取值范围为 _________.
的取值范围为 _________.  (
( ),若
),若 ,则
,则 的值为___________.
的值为___________. 为定义在
为定义在 上的偶函数,当
上的偶函数,当 时,有
时,有 ,且当
,且当 时,
时, ,给出下列命题:
,给出下列命题: 的值为
的值为 ;②函数
;②函数 在定义域上为周期是2的周期函数;
在定义域上为周期是2的周期函数; 与函数
与函数 .
. 则
则 _ .
_ . },有下列命题
},有下列命题 ,则f(x)
,则f(x) M;
M; x2),总有
x2),总有 ﹤0成立;
﹤0成立; 是偶函数,直线
是偶函数,直线 与函数
与函数 的图像自左至右依次交于四个不同点
的图像自左至右依次交于四个不同点 、
、 、
、 、
、 ,若
,若 ,则实数
,则实数 的值为________.
的值为________. 满足
满足 ,且当
,且当 时,
时, ,则
,则 .
. ,
, ,则满足不等式
,则满足不等式 的实数
的实数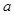 的取值范围是 .
的取值范围是 .