题目内容
求证：
≥
.
思路解析：观察引导的特点，抽象出函数f（x）= 证法一：（分析法）要证明 只需证（|a|+|b|）(1+|a+b|)≥|a+b|(1+|a|+|b|), 只需证|a|+|b|+(|a|+|b|)·|a+b|≥|a+b|+(|a|+|b|)|a+b|, 只需证|a|+|b|≥|a+b|,显然上式成立. 所以原不等式成立. 证法二：（利用函数的单调性）构造函数f(x)= ∵f(x)= ∴函数f(x)在［0,+∞)上随x增大而增大，f(x)是增函数. ∵f(|a|+|b|)= ∴f(|a|+|b|)≥f(|a+b|).∴ 证法三:∵|a+b|≤|a|+|b|,|a+b|=0,显然成立.|a+b|≠0时， 则 深化升华 由上面的证明还可得到以下结论： (1) (2)若|a|≥|b|,则
,利用其单调性证明，还可利用分析法或综合法证明.≥
,
(x≥0).
=1-
,
,f(a+b)= 
,|a|+|b|≥|a+b|,
≥
.
=
≤
=
.
≥
;
≤
.
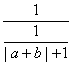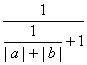练习册系列答案
百校名师阅读真题80篇系列答案
新阅读与作文系列答案
中考全程总复习系列答案
阅读课堂北京教育出版社系列答案
1日1练口算题卡系列答案
培优新题库系列答案
教材备考笔记系列答案
竖式计算卡系列答案
相关题目