Question

在平面内一动点P到两定点A、B距离之积等于这两定点间距离的一半的平方，求P点轨迹的极坐标方程.

Answer 1

解析：首先根据条件建立合适的极坐标系,结合图形,根据动点满足的关系,建立方程,化简即得所求轨迹的极坐标方程.

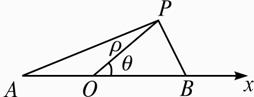
解：如图,以A、B两点连线的中点O为极点,OB射线为极轴建立极坐标系.

设|AB|=2a,则A(a,π),B(a,0),P(ρ,θ),

在△POA和△POB中,

|PA|=

|PB|=.

∵|PA|·|PB|=a²,

∴=a².

化简得ρ²=2a²cos2θ即为所求.