题目内容
一个直角三角形三边的长成等比数列,则( )
| A.三边边长之比为3:4:5 | B.三边边长之比为1:
| ||||||||
C.较小锐角的正弦为
| D.较大锐角的正弦为
|
设直角三角形较短的直角边为a(a>0),公比为q,
由题意得:其它两边分别为aq,aq2,
根据勾股定理得:a2+(aq)2=(aq2)2,
整理得:q4-q2-1=0,
解得:q2=
或q2=
(舍去),
则q2的值为
,
∴三边长之比为a:aq:aq2=1:q:q2=1:
:
,
故选项A和B错误;
设最小内角为α,
根据正弦定理得:
=
,即sinα=
=
=
,
则较小锐角的正弦值为
,故选项C正确,
又最大角为直角,其正弦值为1,故选项D错误,
故选C
由题意得:其它两边分别为aq,aq2,
根据勾股定理得:a2+(aq)2=(aq2)2,
整理得:q4-q2-1=0,
解得:q2=
1+
| ||
| 2 |
1-
| ||
| 2 |
则q2的值为
1+
| ||
| 2 |
∴三边长之比为a:aq:aq2=1:q:q2=1:
|
1+
| ||
| 2 |
故选项A和B错误;
设最小内角为α,
根据正弦定理得:
| a |
| sinα |
| aq2 | ||
sin
|
| 1 |
| q2 |
| 1 | ||||
|
| ||
| 2 |
则较小锐角的正弦值为
| ||
| 2 |
又最大角为直角,其正弦值为1,故选项D错误,
故选C

练习册系列答案
相关题目
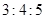 , B.三边边长之比为
, B.三边边长之比为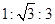 ,
,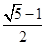 , D.较大锐角的正弦为
, D.较大锐角的正弦为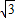 :3
:3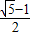
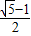
 :3
:3
