题目内容
已知M（1+cos2x，1），N(1，
sin2x+a)（x∈R，a∈R，a是常数），且y=
•
（其中O为坐标原点）．
（1）求y关于x的函数关系式y=f（x）；
（2）求函数y=f（x）的单调区间；
（3）若x∈[0，
]时，f（x）的最大值为4，求a的值．
| 3 |
| OM |
| ON |
（1）求y关于x的函数关系式y=f（x）；
（2）求函数y=f（x）的单调区间；
（3）若x∈[0，
| π |
| 2 |
（1）y=
•
=1+cos2x+
sin2x+a，
所以f(x)=cos2x+
sin2x+1+a．
（2）由（1）可得f(x)=2sin(2x+
)+1+a，
由2kπ-
＜2x+
＜2kπ+
，解得kπ-
＜x＜kπ+
(k∈Z)；
由2kπ+
＜2x+
＜2kπ+
，解得kπ+
＜x＜kπ+
(k∈Z)，
所以f（x）的单调递增区间为[kπ-
，kπ+
](k∈Z)，
单调递减区间为[kπ+
，kπ+
](k∈Z)．
（3）f(x)=2sin(2x+
)+1+a，
因为0≤x≤
，
所以
≤2x+
≤
，
当2x+
=
，即x=
时，f（x）取最大值3+a，
所以3+a=4，即a=1．
| OM |
| ON |
| 3 |
所以f(x)=cos2x+
| 3 |
（2）由（1）可得f(x)=2sin(2x+
| π |
| 6 |
由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
由2kπ+
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
所以f（x）的单调递增区间为[kπ-
| π |
| 3 |
| π |
| 6 |
单调递减区间为[kπ+
| π |
| 6 |
| 2π |
| 3 |
（3）f(x)=2sin(2x+
| π |
| 6 |
因为0≤x≤
| π |
| 2 |
所以
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
当2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
所以3+a=4，即a=1．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
．
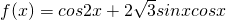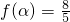，求cos2α的值．