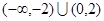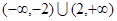题目内容
已知函数 ,满足
,满足 >
> ,则
,则 与
与 的大小关系是( )
的大小关系是( )
 ,满足
,满足 >
> ,则
,则 与
与 的大小关系是( )
的大小关系是( )A. < < | B. > > |
C. = =  | D.不能确定 |
B
试题分析:构造函数
 ,利用导数研究其单调性,注意到已知f'(x)>f(x),可得g(x)为单调增函数,最后由a>0,代入函数解析式即可得答案.∵f'(x)>f(x),
,利用导数研究其单调性,注意到已知f'(x)>f(x),可得g(x)为单调增函数,最后由a>0,代入函数解析式即可得答案.∵f'(x)>f(x),∴g′(x)=
 >0∴函数g(x)为R上的增函数∵a>0∴g(a)>g(0),当a=1,可知成立,故有
>0∴函数g(x)为R上的增函数∵a>0∴g(a)>g(0),当a=1,可知成立,故有 >
> ,选B
,选B点评:本题考查求复合函数的导数的方法,以及指数函数的单调性

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 是定义在
是定义在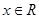 上以2为周期的偶函数,已知
上以2为周期的偶函数,已知 ,
,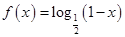 ,则函数
,则函数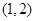 上( )
上( )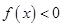
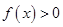
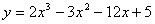 在
在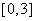 上的最小值是
上的最小值是 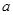 ,
,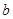 为正实数,函数
为正实数,函数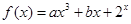 在
在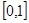 上的最大值为
上的最大值为 ,则
,则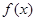 在
在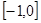 上的最小值为 .
上的最小值为 .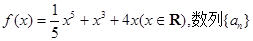 是等差数列,
是等差数列,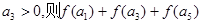 的值
的值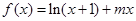 ,当
,当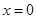 时,函数
时,函数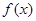 取得极大值.
取得极大值.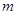 的值;(Ⅱ)已知结论:若函数
的值;(Ⅱ)已知结论:若函数 内导数都存在,且
内导数都存在,且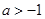 ,则存在
,则存在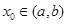 ,使得
,使得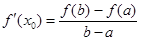 .试用这个结论证明:若
.试用这个结论证明:若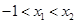 ,函数
,函数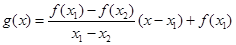 ,则对任意
,则对任意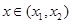 ,都有
,都有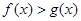 ;(Ⅲ)已知正数
;(Ⅲ)已知正数 满足
满足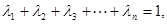 求证:当
求证:当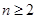 ,
,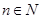 时,对任意大于
时,对任意大于 ,且互不相等的实数
,且互不相等的实数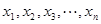 ,都有
,都有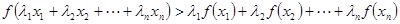
 上的减函数的是( )
上的减函数的是( )


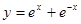
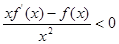 成立,则不等式
成立,则不等式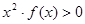 的解集是( )
的解集是( )