题目内容
已知直角三角形的周长为2,则此直角三角形的面积的最大值为________.
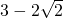
分析:设直角三角形的两直角边为a、b,斜边为c,因为L=a+b+c,c=
 ,两次运用均值不等式即可求解.
,两次运用均值不等式即可求解.解答:直角三角形的两直角边为a、b,斜边为c,面积为s,周长L=2,
由于a+b+
 =L≥2
=L≥2 +
+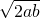 .(当且仅当a=b时取等号)
.(当且仅当a=b时取等号)∴
 ≤
≤ .
.∴S=
 ab≤
ab≤ (
( )2
)2=
 •[
•[ ]2=
]2= L2=
L2=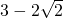 .
.故答案为:
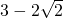 .
.点评:利用均值不等式解决实际问题时,列出有关量的函数关系式或方程式是均值不等式求解或转化的关键.

练习册系列答案
相关题目