题目内容
已知双曲线的一条渐近线方程是x-2y=0,且过点P(4,3),求双曲线的标准方程.
解:根据题意,双曲线的一条渐近线方程为x-2y=0,
设双曲线方程为 -y2=λ(λ≠0),
-y2=λ(λ≠0),
∵双曲线过点P(4,3),
∴ -32=λ,即λ=-5.
-32=λ,即λ=-5.
∴所求双曲线方程为 -y2=-5,
-y2=-5,
即: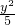 -
-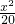 =1.
=1.
分析:根据题意,双曲线的一条渐近线方程为x-2y=0,可设双曲线方程为 -y2=λ(λ≠0),又由双曲线过点P(4,3),将点P的坐标代入可得λ的值,进而可得答案.
-y2=λ(λ≠0),又由双曲线过点P(4,3),将点P的坐标代入可得λ的值,进而可得答案.
点评:本题考查双曲线的标准方程的求法,需要学生熟练掌握已知渐近线方程时,如何设出双曲线的标准方程.
设双曲线方程为
 -y2=λ(λ≠0),
-y2=λ(λ≠0),∵双曲线过点P(4,3),
∴
 -32=λ,即λ=-5.
-32=λ,即λ=-5.∴所求双曲线方程为
 -y2=-5,
-y2=-5,即:
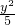 -
-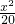 =1.
=1.分析:根据题意,双曲线的一条渐近线方程为x-2y=0,可设双曲线方程为
 -y2=λ(λ≠0),又由双曲线过点P(4,3),将点P的坐标代入可得λ的值,进而可得答案.
-y2=λ(λ≠0),又由双曲线过点P(4,3),将点P的坐标代入可得λ的值,进而可得答案.点评:本题考查双曲线的标准方程的求法,需要学生熟练掌握已知渐近线方程时,如何设出双曲线的标准方程.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 -
- =1(a>0,b>0)的左顶点,且此双曲线的一条渐
=1(a>0,b>0)的左顶点,且此双曲线的一条渐 B.2
B.2 D.2
D.2 分别是双曲线
分别是双曲线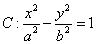
 的左,右焦点。过点
的左,右焦点。过点 与双曲线的一条渐
与双曲线的一条渐 ,且
,且 ,则双曲线的离心率为( )
,则双曲线的离心率为( ) (B)
(B) 
 (D)
(D)
