题目内容
已知m(x2+y2+2y+1)=(x-2y+3)2表示的曲线为一个椭圆,则m的取值范围是分析:根据题意方程表示椭圆,将m(x2+y2+2y+1)=(x-2y+3)2转化为:
=
符合圆锥曲线的统一定义,再根据表示椭圆则比值小于1来求解.
(
| ||||
(
|
| 5 |
| m |
解答:解:∵m(x2+y2+2y+1)=(x-2y+3)2
可转化为:
=
表示动点(x,y)到定点(0,-1)与到定直线x-2y+3=0的距离的平方比为常数
∵表示椭圆,由椭圆定义知比值要小于1
∴
<1,
∴m>5.
故答案为:(5,+∞)
可转化为:
(
| ||||
(
|
| 5 |
| m |
表示动点(x,y)到定点(0,-1)与到定直线x-2y+3=0的距离的平方比为常数
∵表示椭圆,由椭圆定义知比值要小于1
∴
| 5 |
| m |
∴m>5.
故答案为:(5,+∞)
点评:本题主要考查方程的转化与变形,将曲线与方程有机地结合起来,还考查了圆锥曲线的统一定义.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
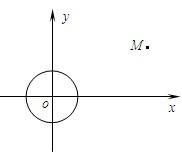 已知⊙O:x2+y2=1和点M(4,2).
已知⊙O:x2+y2=1和点M(4,2). 如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.
如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.