题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,已知sin
A+sinC=psinB(p∈R)且ac=
b2
(1)当
时,求a,c的值;
(2)若角B为锐角,求p的取值范围.
A+sinC=psinB(p∈R)且ac=b2(1)当
时,求a,c的值;(2)若角B为锐角,求p的取值范围.
（1）∵b=1,∴ac=①………………1
又sinA+sinC="psinB " ∴a+c=pb=
②………………3分
解①②得：
………………………6分
（2）∵B为锐角，∴a2+c2＞b2………………………8分
∴(a+c)2-2ac-b2＞0 ∴p2b2-
b2-b2＞0 ∴p2-
＞0
∴p＞
或p＜-(舍)………………………………11分
∴所求p的范围：（，∞）………………………………12分
①………………1又sinA+sinC="psinB " ∴a+c=pb=
②………………3分解①②得：
………………………6分（2）∵B为锐角，∴a2+c2＞b2………………………8分
∴(a+c)2-2ac-b2＞0 ∴p2b2-
b2-b2＞0 ∴p2-＞0∴p＞
或p＜-(舍)………………………………11分∴所求p的范围：（
，∞）………………………………12分略
练习册系列答案
相关题目
中，角
所对的边分别为
，向量
，且
平行，求角
的大小
，求
的面积
在舰
的正东，距离6公里，舰
在舰
的周长为
，且
．
的值；
（结果用反三角函数值表示）．
中，
的对边分别为
，且
．
的值；
，
，求
和
．
C 4 D 4
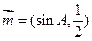与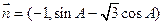
共线，其中A是△ABC的内角。
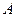的大小； （2）若
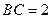，求
的最大值。
中，且
,则△ABC的面积是____
中，
；则符合条件的三角形有 个。