题目内容
已知函数 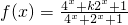 .若对任意的实数x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,则实数k的取值范围是________.
.若对任意的实数x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,则实数k的取值范围是________.
 ≤4
≤4分析:函数
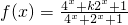 的解析式可化为f(x)=
的解析式可化为f(x)= ,令t=
,令t= ,(t≥3),则f(x)=y=1+
,(t≥3),则f(x)=y=1+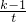 ,结合反比例函数的单调性,分类讨论函数的单调性,并分析出函数的值域,构造关于k的不等式,求出各种情况下实数k的取值范围,最后综合讨论结果,可得实数k的取值范围.
,结合反比例函数的单调性,分类讨论函数的单调性,并分析出函数的值域,构造关于k的不等式,求出各种情况下实数k的取值范围,最后综合讨论结果,可得实数k的取值范围.解答:∵函数
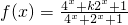 =
=
令t=
 ,(t≥3)
,(t≥3)则f(x)=y=1+
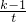
若k-1<0,即k<1,函数y=1+
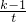 在[3,+∞)上为增函数
在[3,+∞)上为增函数此时的函数f(x)=y值域为[1+
 ,1)
,1)若不等式f(x1)+f(x2)>f(x3)恒成立
则2(1+
 )≥1,就可以满足条件
)≥1,就可以满足条件解得
 <1
<1若k-1=0,即k=1,
f(x)=1,不等式f(x1)+f(x2)>f(x3)显然成立
若k-1>0,即k>1
函数y=1+
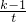 在[3,+∞)上为减函数
在[3,+∞)上为减函数此时的函数f(x)=y值域为(1,1+
 ]
]若不等式f(x1)+f(x2)>f(x3)恒成立
则1+1≥1+
 ,
,解得1<k≤4
综上所述:
 ≤4
≤4故答案为:
 ≤4
≤4点评:本题考查的知识点是函数恒成立问题,指数函数的性质,反比例函数的图象和性质,其中利用换元思想及基本不等式将函数的解析式化为f(x)=y=1+
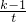 ,是解答的关键.
,是解答的关键. 
练习册系列答案
相关题目
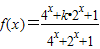 .若对任意的实数x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,则实数k的取值范围是 .
.若对任意的实数x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,则实数k的取值范围是 .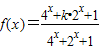 .若对任意的实数x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,则实数k的取值范围是 .
.若对任意的实数x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,则实数k的取值范围是 . ,若存在
,若存在 ,使
,使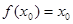 成立,则称
成立,则称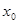 为
为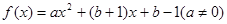 ,若对任意实数b,函数
,若对任意实数b,函数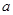 的取值范围是 ( )
的取值范围是 ( ) ,函数
,函数 .
. 在
在 上为减函数,求实数
上为减函数,求实数 的取值范围;
的取值范围;  ,已知函数
,已知函数 .若对任意
.若对任意 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.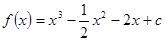 ,若对任意
,若对任意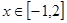 都有
都有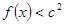 ,则
,则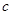 的取值范围是
.
的取值范围是
.