题目内容
如图, 正方形ABCD和ABEF的边长均为1,且它们所在的平面互相垂直,G为BC的中点.
(Ⅰ)求点G到平面ADE的距离;
(Ⅱ)求二面角![]() 的正切值.
的正切值.
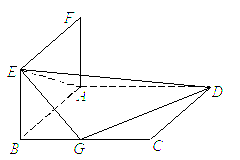
(1)![]() (2)二面角
(2)二面角![]() 的正切值为
的正切值为![]()
解析:
((Ⅰ)∵BC∥AD, AD![]() 面ADE,
面ADE,
∴点G到平面ADE的距离即点B到平面ADE的距离.
连BF交AE于H,则BF⊥AE,又BF⊥AD.
∴BH即点B到平面ADE的距离.)
在Rt△ABE中,![]() .
.
 ∴点G到平面ADE的距离为
∴点G到平面ADE的距离为![]() .
.
(Ⅱ)过点B作BN⊥DG于点N,连EN,
由三垂线定理知EN⊥DN.
∴![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在Rt△BNG中,![]()
∴![]()
则Rt△EBN中,![]()
所以二面角![]() 的正切值为
的正切值为![]() .
.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 (2010•衡阳模拟)如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC.
(2010•衡阳模拟)如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC. 如图,正方形ABCD的边长为1,正方形ADEF所在平面与平面ABCD互相垂直,G,H是DF,FC的中点.
如图,正方形ABCD的边长为1,正方形ADEF所在平面与平面ABCD互相垂直,G,H是DF,FC的中点.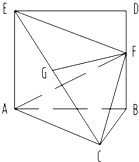 (2011•武进区模拟)如图,正方形ABDE与等边△ABC所在平面互相垂直,AB=2,F为BD中点,G为CE中点.
(2011•武进区模拟)如图,正方形ABDE与等边△ABC所在平面互相垂直,AB=2,F为BD中点,G为CE中点.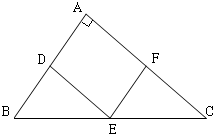 如图,Rt△ABC内有一内接正方形ADEF,它的两条边AD,AF分别在直角边AB,AC上.设BC=a,∠ABC=θ.
如图,Rt△ABC内有一内接正方形ADEF,它的两条边AD,AF分别在直角边AB,AC上.设BC=a,∠ABC=θ.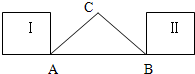 如图,在△ABC中,∠C=90°,
如图,在△ABC中,∠C=90°,