题目内容
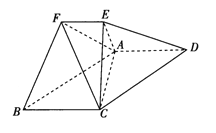
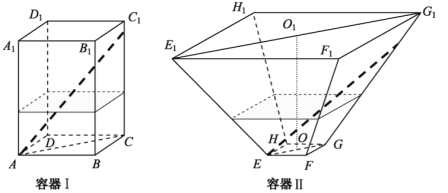
【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10![]() cm,容器Ⅱ的两底面对角线
cm,容器Ⅱ的两底面对角线![]() ,
,![]() 的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(1)将![]() 放在容器Ⅰ中,
放在容器Ⅰ中,![]() 的一端置于点A处,另一端置于侧棱
的一端置于点A处,另一端置于侧棱![]() 上,求
上,求![]() 没入水中部分的长度;
没入水中部分的长度;
(2)将![]() 放在容器Ⅱ中,
放在容器Ⅱ中,![]() 的一端置于点E处,另一端置于侧棱
的一端置于点E处,另一端置于侧棱![]() 上,求
上,求![]() 没入水中部分的长度.
没入水中部分的长度.
【答案】(1)16;(2)20.
【思路分析】(1)转化为直角三角形ACM中,利用相似性质求解AP1;(2)转化到三角形EGN中,先利用直角梯形性质求角![]() ,再利用正弦定理求角
,再利用正弦定理求角![]() ,最后根据直角三角形求高,即为
,最后根据直角三角形求高,即为![]() 没入水中部分的长度.
没入水中部分的长度.
【解析】(1)由正棱柱的定义,![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,![]() .
.
记玻璃棒的另一端落在![]() 上点
上点![]() 处.
处.
因为![]() ,所以
,所以![]() ,从而
,从而![]() ,
,
如图,![]() 与水面的交点为
与水面的交点为![]() ,过
,过![]() 作P1Q1⊥AC,Q1为垂足,
作P1Q1⊥AC,Q1为垂足,
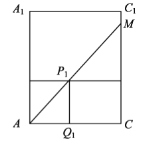
则P1Q1⊥平面ABCD,故P1Q1=12,从而AP1=![]() .
.
答:玻璃棒l没入水中部分的长度为16cm.(5分)
(如果将“没入水中部分”理解为“水面以上部分”,则结果为24cm)
(2)如图,O,O1是正棱台的两底面中心.
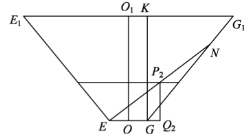
由正棱台的定义,OO1⊥平面EFGH,所以平面E1EGG1⊥平面EFGH,O1O⊥EG.
同理,平面E1EGG1⊥平面E1F1G1H1,O1O⊥E1G1.
记玻璃棒的另一端落在GG1上点N处.
过G作GK⊥E1G1,K为垂足,则GK =OO1=32.
因为EG = 14,E1G1= 62,
所以KG1=![]() ,从而
,从而![]() .
.
设![]() 则
则![]() .
.
因为![]() ,所以
,所以![]() .
.
在![]() 中,由正弦定理可得
中,由正弦定理可得![]() ,解得
,解得![]() .
.
因为![]() ,所以
,所以![]() .
.
于是![]() .
.
记EN与水面的交点为P2,过P2作P2Q2⊥EG,Q2为垂足,则P2Q2⊥平面EFGH,
故P2Q2=12,从而EP2=![]() .
.
答:玻璃棒l没入水中部分的长度为20cm.(10分)
(如果将“没入水中部分”理解为“水面以上部分”,则结果为20cm)

 快乐5加2金卷系列答案
快乐5加2金卷系列答案【题目】“累计净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为![]() 时对颗粒物的累计净化量(单位:克).根据国家标准,对空气净化器的累计净化量(CCM)有如下等级划分:
时对颗粒物的累计净化量(单位:克).根据国家标准,对空气净化器的累计净化量(CCM)有如下等级划分:
累计净化量(克) |
|
|
| 12以上 |
等级 |
|
|
|
|
已知某批空气净化器共![]() 台,其累计净化量都分布在区间
台,其累计净化量都分布在区间![]() 内,为了解其质量,随机抽取了
内,为了解其质量,随机抽取了![]() 台净化器作为样本进行估计,按照
台净化器作为样本进行估计,按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 均匀分组,其中累计净化量在
均匀分组,其中累计净化量在![]() 的所有数据有:
的所有数据有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() ,并绘制了如下频率分布直方图.
,并绘制了如下频率分布直方图.
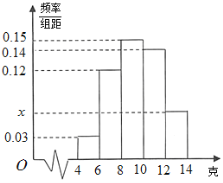
(1)求![]() 的值及频率分布直方图中
的值及频率分布直方图中![]() 的值;
的值;
(2)以样本估计总体,试估计这批空气净化器(共2000台)中等级为![]() 的空气净化器有多少台?
的空气净化器有多少台?
(3)从累计净化量在![]() 的样本中随机抽取2台,求恰好有1台等级为
的样本中随机抽取2台,求恰好有1台等级为![]() 的概率.
的概率.