题目内容
已知数列{an}中,a1=1,前n项和为Sn且Sn+1= Sn+1,n∈N*.
Sn+1,n∈N*.
(1)求数列{an}的通项公式.
(2)求数列{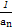 }的前n项和Tn.
}的前n项和Tn.
 Sn+1,n∈N*.
Sn+1,n∈N*.(1)求数列{an}的通项公式.
(2)求数列{
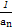 }的前n项和Tn.
}的前n项和Tn.(1) an=( )n-1 (2) Tn=3[1-(
)n-1 (2) Tn=3[1-( )n]
)n]
 )n-1 (2) Tn=3[1-(
)n-1 (2) Tn=3[1-( )n]
)n](1)由Sn+1= Sn+1,
Sn+1,
得当n≥2时Sn= Sn-1+1,
Sn-1+1,
∴Sn+1-Sn= (Sn-Sn-1),
(Sn-Sn-1),
即an+1= an,∴
an,∴ =
= ,
,
又a1=1,得S2= a1+1=a1+a2,∴a2=
a1+1=a1+a2,∴a2= ,
,
∴ =
= ,
,
∴数列{an}是首项为1,公比为 的等比数列,
的等比数列,
∴an=( )n-1.
)n-1.
(2)∵数列{an}是首项为1,公比为 的等比数列,
的等比数列,
∴数列{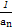 }是首项为1,公比为
}是首项为1,公比为 的等比数列,
的等比数列,
∴Tn= =3[1-(
=3[1-( )n].
)n].
 Sn+1,
Sn+1,得当n≥2时Sn=
 Sn-1+1,
Sn-1+1,∴Sn+1-Sn=
 (Sn-Sn-1),
(Sn-Sn-1),即an+1=
 an,∴
an,∴ =
= ,
,又a1=1,得S2=
 a1+1=a1+a2,∴a2=
a1+1=a1+a2,∴a2= ,
,∴
 =
= ,
,∴数列{an}是首项为1,公比为
 的等比数列,
的等比数列,∴an=(
 )n-1.
)n-1.(2)∵数列{an}是首项为1,公比为
 的等比数列,
的等比数列,∴数列{
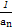 }是首项为1,公比为
}是首项为1,公比为 的等比数列,
的等比数列,∴Tn=
 =3[1-(
=3[1-( )n].
)n].
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
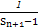 ,其前n项和为Tn,求证:Tn<
,其前n项和为Tn,求证:Tn< (n∈N*).
(n∈N*). 是较小的两份之和,则最小的一份为( )
是较小的两份之和,则最小的一份为( )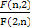 (n∈N*),若对任意正整数n,都有an≥ak(k∈N*)成立,则ak的值为( )
(n∈N*),若对任意正整数n,都有an≥ak(k∈N*)成立,则ak的值为( )
 的前
的前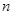 项和
项和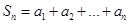 ,若
,若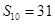 ,
,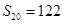 ,则
,则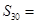 ( )
( )