题目内容
若x>0,y>0,x+y>2,求证: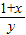 <2,
<2,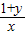 <2至少有一个成立.
<2至少有一个成立.
【答案】分析:运用反证法,假设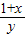 <2,
<2,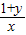 <2均不成立,则
<2均不成立,则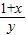 ≥2,
≥2,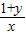 ≥2,从而可得x+y≤2,这和已知条件x+y>2相矛盾,即可得到结论.
≥2,从而可得x+y≤2,这和已知条件x+y>2相矛盾,即可得到结论.
解答:证明:假设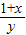 <2,
<2,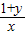 <2均不成立,则
<2均不成立,则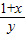 ≥2,
≥2,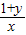 ≥2,
≥2,
∴1+x≥2y,1+y≥2x,
∴1+x+1+y≥2y+2x,
∴x+y≤2,这和已知条件x+y>2相矛盾,所以假设不成立,
∴原命题成立.
点评:本题考查不等式的证明,考查反证法的运用,正确引出矛盾是关键.
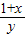 <2,
<2,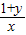 <2均不成立,则
<2均不成立,则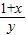 ≥2,
≥2,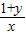 ≥2,从而可得x+y≤2,这和已知条件x+y>2相矛盾,即可得到结论.
≥2,从而可得x+y≤2,这和已知条件x+y>2相矛盾,即可得到结论.解答:证明:假设
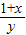 <2,
<2,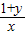 <2均不成立,则
<2均不成立,则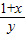 ≥2,
≥2,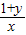 ≥2,
≥2,∴1+x≥2y,1+y≥2x,
∴1+x+1+y≥2y+2x,
∴x+y≤2,这和已知条件x+y>2相矛盾,所以假设不成立,
∴原命题成立.
点评:本题考查不等式的证明,考查反证法的运用,正确引出矛盾是关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
 A(不等式选做题)若x>0,y>0且x+2y=1,则
A(不等式选做题)若x>0,y>0且x+2y=1,则