题目内容
设A(x1,x2)、B(x2,y2)是抛物线x2=4y上不同的两点,且该抛物线在点A、B处的两条切线相交于点C,并且满足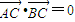 .
.(1)求证:x1•x2=-4;
(2)判断抛物线x2=4y的准线与经过A、B、C三点的圆的位置关系,并说明理由.
【答案】分析:(1)先求出抛物线方程的导函数,进而设出点A、B处的切线的斜率;再利用 得到
得到 ,即可得到关于点A、B横坐标之间的等量关系,即可证明结论.
,即可得到关于点A、B横坐标之间的等量关系,即可证明结论.
(2)先利用 得经过A、B、C三点的圆的圆心为线段AB的中点D,利用中点坐标公式求出点D;再利用两点间的距离公式求出圆的半径的表达式,整理即可得到抛物线x2=4y的准线与经过A、B、C三点的圆的位置关系.
得经过A、B、C三点的圆的圆心为线段AB的中点D,利用中点坐标公式求出点D;再利用两点间的距离公式求出圆的半径的表达式,整理即可得到抛物线x2=4y的准线与经过A、B、C三点的圆的位置关系.
解答:证明:(1)由x2=4y得 ,则
,则 ,
,
∴抛物线x2=4y在点A(x1,x2)、B(x2,y2)处的切线的斜率分别为 ,…(2分)
,…(2分)
∵ ,∴
,∴ ,…(4分)
,…(4分)
∴抛物线x2=4y在点A(x1,x2)、B(x2,y2)处两切线互相垂直,
∴ ,
,
∴x1•x2=-4.…(6分)
解:(2)∵ ,
,
∴ ,
,
∴经过A、B、C三点的圆的圆心为线段AB的中点D,
圆心D ,…(8分)
,…(8分)
∵抛物线x2=4y的准线方程为y=-1,
∴点D 到直线
到直线
y=-1的距离为 ,…(10分)
,…(10分)
∵经过A、B、C三点的圆的半径 ,
,
由于x12=4y1,x22=4y2,且x1•x2=-4,则 ,
,
∴
=
=
=
= ,…(12分)
,…(12分)
∴d=r,
∴抛物线x2=4y准线与经过A、B、C三点的圆相切.…(14分)
点评:本题主要考查直线与圆锥曲线的综合问题,做这一类型题目的关键是看清题中给出的条件,灵活运用中点坐标公式以及点到直线的距离公式,抛圆锥曲线的定义进行求解.
 得到
得到 ,即可得到关于点A、B横坐标之间的等量关系,即可证明结论.
,即可得到关于点A、B横坐标之间的等量关系,即可证明结论.(2)先利用
 得经过A、B、C三点的圆的圆心为线段AB的中点D,利用中点坐标公式求出点D;再利用两点间的距离公式求出圆的半径的表达式,整理即可得到抛物线x2=4y的准线与经过A、B、C三点的圆的位置关系.
得经过A、B、C三点的圆的圆心为线段AB的中点D,利用中点坐标公式求出点D;再利用两点间的距离公式求出圆的半径的表达式,整理即可得到抛物线x2=4y的准线与经过A、B、C三点的圆的位置关系.解答:证明:(1)由x2=4y得
 ,则
,则 ,
,∴抛物线x2=4y在点A(x1,x2)、B(x2,y2)处的切线的斜率分别为
 ,…(2分)
,…(2分)∵
 ,∴
,∴ ,…(4分)
,…(4分)∴抛物线x2=4y在点A(x1,x2)、B(x2,y2)处两切线互相垂直,
∴
 ,
,∴x1•x2=-4.…(6分)
解:(2)∵
 ,
,∴
 ,
,∴经过A、B、C三点的圆的圆心为线段AB的中点D,
圆心D
 ,…(8分)
,…(8分)∵抛物线x2=4y的准线方程为y=-1,
∴点D
 到直线
到直线y=-1的距离为
 ,…(10分)
,…(10分)∵经过A、B、C三点的圆的半径
 ,
,由于x12=4y1,x22=4y2,且x1•x2=-4,则
 ,
,∴

=

=

=

=
 ,…(12分)
,…(12分)∴d=r,
∴抛物线x2=4y准线与经过A、B、C三点的圆相切.…(14分)
点评:本题主要考查直线与圆锥曲线的综合问题,做这一类型题目的关键是看清题中给出的条件,灵活运用中点坐标公式以及点到直线的距离公式,抛圆锥曲线的定义进行求解.

练习册系列答案
相关题目