题目内容
已知|a|＝4，|b|＝3，(2a－3b)·(2a＋b)＝61．
(1)求a与b的夹角θ；
(2)求|a＋b|；
(3)若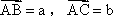
，作△ABC，求△ABC的面积．
答案：
解析：
解析：
|
解：(1)用夹角公式计算 由(2a－3b)·(2a＋b)＝61，得4|a|2－4a·b－3|b|2＝61． ∵|a|＝4，|b|＝3，代入上式求得a·b＝－6． 又θ∈[0°，180°]，∴θ＝120°． (2)可先平方转化为向量的数量积． |a＋b|2＝(a＋b)2＝|a|2＋2a·b＋|b|2
(3)计算a，b夹角的正弦，再用面积公式求值． |
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
＝a，
＝b，求△ABC的面积．
D.2
(2a＋b)＝61．